题目内容
已知函数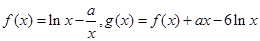 ,其中
,其中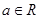 .
.
(1)当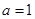 时判断
时判断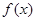 的单调性;
的单调性;
(2)若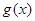 在其定义域为增函数,求正实数
在其定义域为增函数,求正实数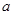 的取值范围;
的取值范围;
(3)设函数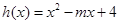 ,当
,当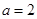 时,若
时,若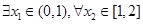 ,总有
,总有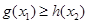 成立,求实数
成立,求实数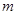 的取值范围.
的取值范围.
【答案】
(1)增函数;(2) ;(3)
;(3)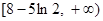 .
.
【解析】
试题分析:(1) 本小题首先求得函数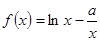 的定义域
的定义域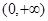 ,再利用导数的公式和法则求得函数
,再利用导数的公式和法则求得函数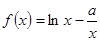 的导函数
的导函数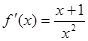 ,发现其在
,发现其在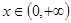 恒大于零,于是可知函数
恒大于零,于是可知函数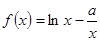 在
在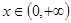 上单调递增;(2) 本小题首先求得函数
上单调递增;(2) 本小题首先求得函数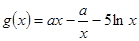 的定义域
的定义域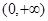 ,再利用导数的公式和法则求得函数
,再利用导数的公式和法则求得函数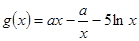 的导函数
的导函数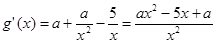 ,根据函数
,根据函数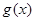 在其定义域内为增函数,所以
在其定义域内为增函数,所以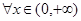 ,
,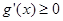 ,然后转化为最值得求解;(3)本小题首先分析“
,然后转化为最值得求解;(3)本小题首先分析“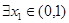 ,
,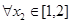 ,总有
,总有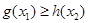 成立”等价于 “
成立”等价于 “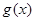 在
在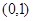 上的最大值不小于
上的最大值不小于 在
在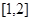 上的最大值”,于是问题就转化为求函数的最值.
上的最大值”,于是问题就转化为求函数的最值.
试题解析:(1)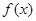 的定义域为
的定义域为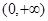 ,且
,且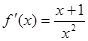 >0
>0
所以f(x)为增函数. 3分
(2)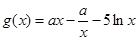 ,
,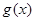 的定义域为
的定义域为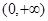
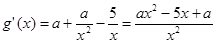 5分
5分
因为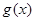 在其定义域内为增函数,所以
在其定义域内为增函数,所以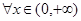 ,
,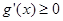
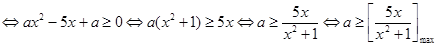
而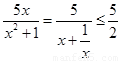 ,当且仅当
,当且仅当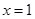 时取等号,所以
时取等号,所以 9分
9分
(3)当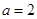 时,
时,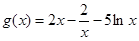 ,
,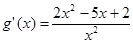
由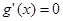 得
得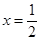 或
或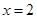
当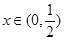 时,
时,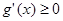 ;当
;当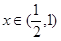 时,
时,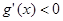 .
.
所以在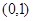 上,
上, 11分
11分
而“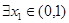 ,
,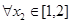 ,总有
,总有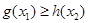 成立”等价于
成立”等价于
“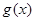 在
在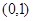 上的最大值不小于
上的最大值不小于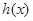 在
在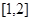 上的最大值”
上的最大值”
而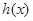 在
在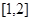 上的最大值为
上的最大值为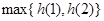
所以有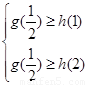
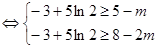
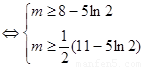
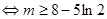
所以实数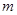 的取值范围是
的取值范围是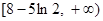 14分
14分
考点:1.导数公式与法则;2.函数的单调性;3.等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目






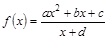 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.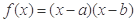 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
