题目内容
已知点![]() 和互不相同的点
和互不相同的点![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,满足
,…,满足![]() ,其中
,其中![]() 分别为等差数列和等比数列,
分别为等差数列和等比数列,![]() 为坐标原点,若
为坐标原点,若![]() 是线段
是线段![]() 的中点.
的中点.
(1)求![]() 的值;
的值;
(2)点![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…能否共线?证明你的结论;
,…能否共线?证明你的结论;
(3)证明:对于给定的公差不零的![]() ,都能找到唯一的一个
,都能找到唯一的一个![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,都在一个指数函数的图象上.
,…,都在一个指数函数的图象上.
解:(1)![]() 是线段
是线段![]() 的中点
的中点 ![]()
又![]() , 且
, 且![]() 不共线,
不共线,
由平面向量基本定理,知:![]()
(2) 由![]()
设![]() 的公差为
的公差为![]() ,
,![]() 的公比为
的公比为![]() ,则由于
,则由于![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…互不相同,
,…互不相同,
所以![]() ,
,![]() 不会同时
不会同时![]() 成立;
成立;
若![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…都在直线
,…都在直线![]() 上;
上;
若![]() ,则
,则![]() 为常数列,
为常数列,
![]()
![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…都在直线
,…都在直线![]() 上;
上;
若![]() 且
且![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…共线
,…共线
![]()
![]()
![]() 与
与![]() 共线(
共线(![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与
与![]() 矛盾,
矛盾,
∴当![]() 且
且![]() 时,
时,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…不共线.
,…不共线.
(3)设![]() 都在指数函数
都在指数函数![]() 的图像上,则
的图像上,则![]()
![]() 令
令![]() ,则
,则![]() ,
,
于是,![]() 有唯一解
有唯一解![]() ,
,
由于![]() ,
, ![]() ,从而满足条件“
,从而满足条件“![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…互不相同”。
,…互不相同”。
∴当对于给定的![]() ,都能找到唯一的一个
,都能找到唯一的一个![]() ,
,
使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…,都在指数函数
,…,都在指数函数![]() 的图象上。
的图象上。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 和互不相同的点
和互不相同的点 ,
, ,其中
,其中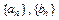 分别为等差数列和等比数列,O为坐标原点,若
分别为等差数列和等比数列,O为坐标原点,若 为线段AB的中点。
为线段AB的中点。 的值;
的值; 的公差为d =0,或
的公差为d =0,或 的公比为q=1,点
的公比为q=1,点 0,且q
0,且q  和互不相同的点
和互不相同的点 ,
, ,
, ,…,
,…, ,…,满足
,…,满足 ,
, 为坐标原点,其中
为坐标原点,其中 分别为等差数列和等比数列,
分别为等差数列和等比数列, 的中点,对于给定的公差不为零的
的中点,对于给定的公差不为零的 ,都能找到唯一的一个
,都能找到唯一的一个 ,使得
,使得 和互不相同的点
和互不相同的点 ,
, ,
, ,…,
,…, ,…,满足
,…,满足 ,
, 为坐标原点,其中
为坐标原点,其中 分别为等差数列和等比数列,若
分别为等差数列和等比数列,若 的中点,设等差数列公差为
的中点,设等差数列公差为 ,等比数列公比为
,等比数列公比为 ,当
,当 和互不相同的点
和互不相同的点 ,
, ,
, ,…,
,…, ,…,满足
,…,满足 ,
, 为坐标原点,其中
为坐标原点,其中 分别为等差数列和等比数列,若
分别为等差数列和等比数列,若 的中点,设等差数列公差为
的中点,设等差数列公差为 ,等比数列公比为
,等比数列公比为 ,当
,当 和互不相同的点
和互不相同的点 ,
, ,
, ,…,
,…, ,…,满足
,…,满足 ,
, 为坐标原点,其中
为坐标原点,其中 分别为等差数列和等比数列,
分别为等差数列和等比数列,  的中点,对于给定的公差不为零的
的中点,对于给定的公差不为零的 ,都能找到唯一的一个
,都能找到唯一的一个 ,使得
,使得