题目内容
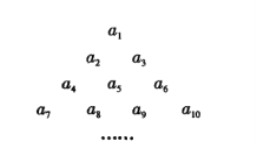
【题目】将各项均为整数的数列![]() 排成如图所示的三角形数阵(第
排成如图所示的三角形数阵(第![]() 行有
行有![]() 个数,同一行中,下标小的数排在左边).
个数,同一行中,下标小的数排在左边).![]() 表示数阵中第
表示数阵中第![]() 行第1列的数.
行第1列的数.
已知数列![]() 为等比数列,且从第3行开始,各行均构成公差为
为等比数列,且从第3行开始,各行均构成公差为![]() 的等差数列,
的等差数列,![]() ,
,![]() ,
,![]() .
.
(1)求数阵中第![]() 行 第
行 第![]() 列的数
列的数 ![]() (用
(用 ![]() 、
、![]() 表示);
表示);
(2)求![]() 的值;
的值;
(3)2013是否在该数阵中,说明理由.
【答案】(1) ![]() (2)
(2) ![]() (3) 2013不再该数阵中
(3) 2013不再该数阵中
【解析】
(1)设![]() 的公比为
的公比为![]() .
.
依题意,![]() 为数阵中第5行第2列的数;
为数阵中第5行第2列的数;![]() 为数阵中第6行第3列的数.
为数阵中第6行第3列的数.
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
于是,![]() ,
,![]() ,
,![]() .
.
故![]() .
.
(2)由1+2+…+62=1953,
1+2+…+63=2016,
2013-1953=60,
知![]() 为数阵中第63行第60列的数.
为数阵中第63行第60列的数.
从而,![]() .
.
(3)假设2013为数阵中第![]() 行第
行第![]() 列的数.
列的数.
由第![]() 行中最小的数为
行中最小的数为![]() 、最大的数为
、最大的数为![]() ,知
,知
![]() ①
①
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
于是,不等式①无正整数解.
从而,2013不再该数阵中.

练习册系列答案
相关题目