题目内容
设x=3是函数f(x)=
，(a＞0，x∈R)的一个极值点．
（1）求a与b的关系式（用a表示b），并求f（x）的单调递增区间；
（2）设g(x)=(a2+
)ex，若存在x1，x2∈[0，4]使得|f（x1）-g（x2）|＜1成立，求实数a的取值范围．
| e3(x2+ax+b) |
| ex |
（1）求a与b的关系式（用a表示b），并求f（x）的单调递增区间；
（2）设g(x)=(a2+
| 25 |
| 4 |
分析：（1）由已知中函数f(x)=
，(a＞0，x∈R)的一个极值点是x=3．我们根据函数在某点取得极值的条件，易得f′（3）=0，进而构造方程求出a与b的关系式，分析函数在各个区间上的符号，即可得到答案．
（2）根据g(x)=(a2+
)ex，利用导数法确定函数的单调性，再根据（1）的结论，我们可以构造一个关于a的不等式，解不等式即可得到答案．
| e3(x2+ax+b) |
| ex |
（2）根据g(x)=(a2+
| 25 |
| 4 |
解答：解：（1）∵f(x)=
，(x∈R)，
∴f′(x)=
，
∵函数f(x)=
，(a＞0，x∈R)的一个极值点是x=3．
∴f′(3)=
=0，
∴b=-2a-3，
∵a＞0，令f′(x)=
＞0，
即x2-（2-a）x-（3+1）a＜0
解得：-1-a＜x＜3，
所以f（x）的单调递增区间是：[-1-a，3]；
（2）由（1）可得，函数f（x）在[0，3]上单调递增，在[3，4]上单调递减，
∴fmax（x）=f（3）=a+6，且f(0)=-(2a+3)e3＜f(4)=
∴函数f（x）在x∈[0，4]的值域为[-（2a+3）e3，a+6]，
又g′(x)=(a2+
)ex＞0，
∴g（x）在[0，4]上单调递增，
故g（x）在x∈[0，4]的值域为[a2+
，(a2+
)e4]，
若存在x1，x2∈[0，4]使得|f（x1）-g（x2）|＜1成立，
等价于|fmax（x）-gmin（x）|＜1或|gmax（x）-fmin（x）|＜1，
又∵a2+
≥a+6，
于是：
，
解得：0＜a＜
；
∴实数a的取值范围是：(0，
)．
| e3(x2+ax+b) |
| ex |
∴f′(x)=
| e3(-x2+2x-ax+a-b) |
| ex |
∵函数f(x)=
| e3(x2+ax+b) |
| ex |
∴f′(3)=
| e3(-32+2×3-3a+a-b) |
| e3 |
∴b=-2a-3，
∵a＞0，令f′(x)=
| e3(-x2+2x-ax+3a+3) |
| ex |
即x2-（2-a）x-（3+1）a＜0
解得：-1-a＜x＜3，
所以f（x）的单调递增区间是：[-1-a，3]；
（2）由（1）可得，函数f（x）在[0，3]上单调递增，在[3，4]上单调递减，
∴fmax（x）=f（3）=a+6，且f(0)=-(2a+3)e3＜f(4)=
| e3(13+2a) |
| e4 |
∴函数f（x）在x∈[0，4]的值域为[-（2a+3）e3，a+6]，
又g′(x)=(a2+
| 25 |
| 4 |
∴g（x）在[0，4]上单调递增，
故g（x）在x∈[0，4]的值域为[a2+
| 25 |
| 4 |
| 25 |
| 4 |
若存在x1，x2∈[0，4]使得|f（x1）-g（x2）|＜1成立，
等价于|fmax（x）-gmin（x）|＜1或|gmax（x）-fmin（x）|＜1，
又∵a2+
| 25 |
| 4 |
于是：
|
解得：0＜a＜
| 3 |
| 2 |
∴实数a的取值范围是：(0，
| 3 |
| 2 |
点评：本题考查的知识点是函数在某点取得极值的条件，利用导数研究函数的单调性，其中根据已知中的函数的解析式，结合导数公式，求出函数的导函数的解析式，是解答本题的关键．
练习册系列答案
应用题作业本系列答案
相关题目
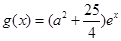，若存在ε1，ε2∈[0，4]，使｜f (ε1)-g (ε2)｜<1成立，求a的取值范围。
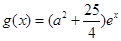，若存在ε1，ε2∈[0，4]，使｜f (ε1)-g (ε2)｜<1成立，求a的取值范围