题目内容
12.若函数$f(x)=-\frac{1}{2}{({x-2})^2}+alnx$在(1,+∞)上是减函数,则实数a的取值范围是( )| A. | .[-1,+∞) | B. | (-∞,-1] | C. | (1,+∞) | D. | .(-∞,1] |
分析 求出函数的导函数,利用导函数的符号,得到a的不等式,然后求解实数a的取值范围.
解答 解:函数$f(x)=-\frac{1}{2}{({x-2})^2}+alnx$,x∈(1,+∞),
可得f′(x)=x-2+$\frac{a}{x}$,
函数$f(x)=-\frac{1}{2}{({x-2})^2}+alnx$在(1,+∞)上是减函数,
可得-x+2+$\frac{a}{x}$<0,在x∈(1,+∞)上恒成立,
即a<x2-2x在x∈(1,+∞)上恒成立,
函数g(x)=x2-2x的对称轴为:x=1,在x∈(1,+∞)上是增函数,函数的最小值为:g(1)=1.
可得a≤1.
实数a的取值范围是:(-∞,1].
故选:B.
点评 本题考查函数的导数的综合应用,函数恒成立,考查计算能力以及转化思想的应用.

练习册系列答案
相关题目
1.用秦九韶算法求多项式f(x)=2+0.35x+1.8x2-3.66x3+6x4-5.2x5+x6,在x=-1.3的值时,令v0=a6,v1=v0x+a5,…,v6=v5x+a0,则v3的值是 ( )
| A. | -9.8205 | B. | 14.25 | C. | -22.445 | D. | 30.9785 |
19.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-bx+c\\;x≥0}\\{{e}^{x}\\;x<0}\end{array}\right.$,其中b=$\frac{2}{π}$${∫}_{-2}^{2}$$\sqrt{4-{x}^{2}}$dx,c为目标函数z=2x+4y在约束条件$\left\{\begin{array}{l}{y≥0}\\{x+y-1≤0}\\{x-y+2≥0}\end{array}\right.$,内的最大值,则f(x)<10的解集为( )
| A. | (-∞,0) | B. | [0,5) | C. | (-∞,5) | D. | (-∞,5] |
4.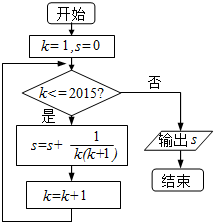 执行如图所示的程序框图,输出的s为( )
执行如图所示的程序框图,输出的s为( )
 执行如图所示的程序框图,输出的s为( )
执行如图所示的程序框图,输出的s为( )| A. | $\frac{2015}{2016}$ | B. | $\frac{2014}{2015}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2017}{2016}$ |