题目内容
对于正项数列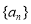 ,若
,若 对一切
对一切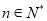 恒成立,则
恒成立,则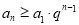 对
对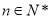 也恒成立是真命题.
也恒成立是真命题.
(1)若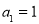 ,
,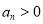 ,且
,且 ,求证:数列
,求证:数列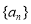 前
前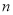 项和
项和 ;
;
(2)若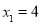 ,
,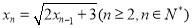 ,求证:
,求证: .
.
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据题中定义,结合 得到
得到 ,再利用等比数列的求和公式进行求和证明;(2)利用分子有理化化简得到
,再利用等比数列的求和公式进行求和证明;(2)利用分子有理化化简得到 ,进一步推得
,进一步推得 ,再利用等比数列的求和公式进行证明.
,再利用等比数列的求和公式进行证明.
试题解析:(1) , 2分
, 2分
 , 4分
, 4分
 , 6分
, 6分
 ; 7分
; 7分
(2) , 10分
, 10分
 , 11分
, 11分
 , 12分
, 12分
 13分
13分
 .
.
考点:1.新定义型题目;2.等比数列;3.放缩法.
考点分析: 考点1:等比数列 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
相关题目
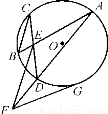
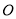 的两弦
的两弦 和
和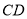 交于点
交于点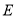 ,
,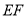 ∥
∥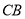 ,
,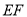 交
交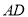 的延长线于点
的延长线于点 ,
,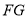 切圆
切圆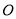 于点
于点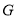 .
. 
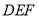 ∽△
∽△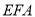 ;
;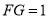 ,求
,求 ,则输出
,则输出 的值为( )
的值为( )
 上的两点
上的两点 、
、 到焦点的距离之和为6,则线段
到焦点的距离之和为6,则线段 的中点到
的中点到 轴的距离为 .
轴的距离为 . 满足
满足 32,则
32,则 的最小值为 .
的最小值为 . 的奇偶性.
的奇偶性. 是函数
是函数 图像上任意一点,则下列各点中一定在该图像上的是 ( )
图像上任意一点,则下列各点中一定在该图像上的是 ( ) B.
B. C.
C. D.
D.
 ,集合
,集合 ,则
,则 .
. 中,若
中,若 ,
, ,
, ,
, 为
为 中点,点
中点,点
 中点,
中点, 在线段
在线段 上,且
上,且 ,则
,则 的长度为________ .
的长度为________ .