Question

函数y=

- 1 2 x2+x+ 1 2

的图象上存在不同的三点到原点的距离构成等比数列，则下列给定的数中可能是该等比数列的公比的是（　　）

• A、

  1

  3

• B、2
• C、3
• D、

  3

  +1

Answer 1

分析：把函数解析式变形，作出相应的图象，数形结合可知曲线上的点到原点的距离范围，求出工笔的范围后得答案．

解答：解：由y=

- 1 2 x2+x+ 1 2

，
得

(x-1)2

2

+y2=1  (y≥0)，
图象如图，

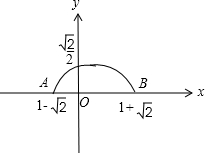
为上半椭圆，图象上距原点最近的点为A，最远的点为B，
则由q2=

2 +1

2 -1

=(

2

+1)2，得q=

2

+1；
或由q2=

2 -1

2 +1

=(

2

-1)2，得q=

2

-1．
可知q∈[

2

-1，

2

+1]，
故选：B．

点评：本题考查了等比数列的通项公式，训练了数形结合的解题思想方法，是基础题．