题目内容
(本小题满分15分)已知函数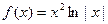 ,
,
(Ⅰ)判断函数
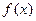 的奇偶性;
的奇偶性;
(Ⅱ)求函数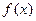 的单调区间;
的单调区间;
(Ⅲ)若关于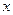 的方
的方
 程
程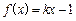 有实数解,求实数
有实数解,求实数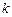 的取值范围.
的取值范围.
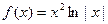 ,
,(Ⅰ)判断函数

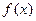 的奇偶性;
的奇偶性;(Ⅱ)求函数
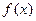 的单调区间;
的单调区间;(Ⅲ)若关于
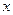 的方
的方
 程
程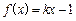 有实数解,求实数
有实数解,求实数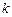 的取值范围.
的取值范围.解:(Ⅰ)函数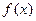 的定义域为{
的定义域为{ 且
且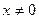 }
}
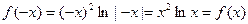 ∴
∴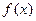 为偶函数
为偶函数
(Ⅱ)当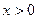 时,
时,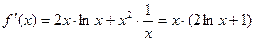
若 ,则
,则 ,
,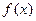 递减;
递减;
若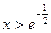 , 则
, 则 ,
,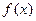 递增.
递增.
再由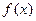 是偶函数,
是偶函数,
得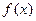 的递增区
的递增区 间是
间是 和
和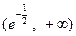 ;
;
递减区间是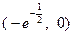 和
和 .
.
(Ⅲ)由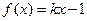 ,得:
,得: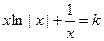 令
令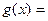
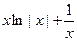
当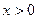 ,
,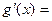
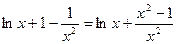 显然
显然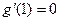
 时,
时,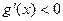 ,
,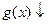
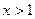 时,
时,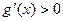 ,
,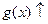
∴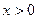 时,
时,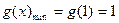
又 ,
,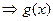 为奇函数 ∴
为奇函数 ∴ 时,
时,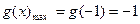
∴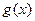 的值域为(-∞,-1]∪[1,+∞)
的值域为(-∞,-1]∪[1,+∞)
∴若方程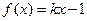 有实数
有实数 解,则实数
解,则实数 的取值范围是(
的取值范围是( -∞,-1]∪[1,+∞).
-∞,-1]∪[1,+∞).
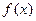 的定义域为{
的定义域为{ 且
且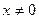 }
} 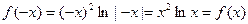 ∴
∴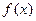 为偶函数
为偶函数 (Ⅱ)当
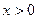 时,
时,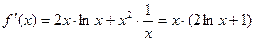
若
 ,则
,则 ,
,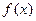 递减;
递减; 若
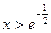 , 则
, 则 ,
,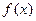 递增.
递增.再由
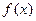 是偶函数,
是偶函数,得
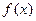 的递增区
的递增区 间是
间是 和
和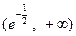 ;
;递减区间是
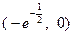 和
和 .
.(Ⅲ)由
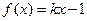 ,得:
,得: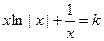 令
令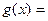
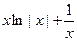
当
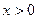 ,
,
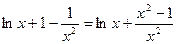 显然
显然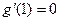
 时,
时,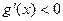 ,
,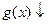
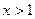 时,
时,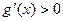 ,
,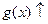
∴
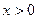 时,
时,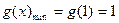
又
 ,
,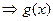 为奇函数 ∴
为奇函数 ∴ 时,
时,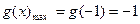
∴
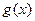 的值域为(-∞,-1]∪[1,+∞)
的值域为(-∞,-1]∪[1,+∞)∴若方程
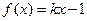 有实数
有实数 解,则实数
解,则实数 的取值范围是(
的取值范围是( -∞,-1]∪[1,+∞).
-∞,-1]∪[1,+∞).略

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
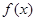 在
在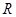 上可导,则
上可导,则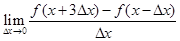 等于( )
等于( )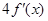
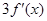
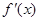
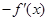
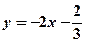 与曲线
与曲线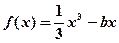 相切
相切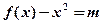 在
在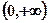 上恰有两个不等的实数根
上恰有两个不等的实数根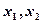 ,求
,求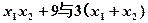 的大小
的大小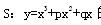 的图象与x轴相切于不同于原点的一点,又函数有极小值-4,求
的图象与x轴相切于不同于原点的一点,又函数有极小值-4,求 的值。
的值。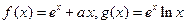 (
(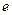 是自然对数的底数).
是自然对数的底数).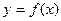 在
在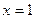 处的切线也是抛物线
处的切线也是抛物线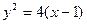 的切线,求
的切线,求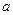 的值;
的值;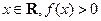 恒成立,试确定实数
恒成立,试确定实数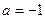 时,是否存在
时,是否存在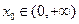 ,使曲线
,使曲线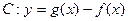 在点
在点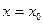 处的切线斜率与
处的切线斜率与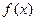 在
在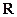 上的最小值相等?若存在,求符合条件的
上的最小值相等?若存在,求符合条件的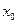 的个数;若不存在,请说明理由.
的个数;若不存在,请说明理由.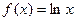
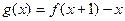 的最大值;
的最大值;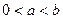 时,求证
时,求证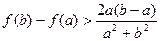 ;
; ):
):
 ;
;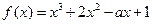 在区间
在区间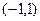 上是单调函数,则实数
上是单调函数,则实数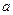 的取值范围是
的取值范围是