题目内容
【题目】在以![]() 为圆心,6为半径的圆
为圆心,6为半径的圆![]() 内有一点
内有一点![]() ,点
,点![]() 为圆
为圆![]() 上的任意一点,线段
上的任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 交于点
交于点![]() .
.
(1)判断点![]() 的轨迹是什么曲线,并求其方程;
的轨迹是什么曲线,并求其方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,过点
,过点![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的最大值;
的最大值;
(3)在圆![]() 上的任取一点
上的任取一点![]() ,作曲线
,作曲线![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 、
、![]() ,试判断
,试判断![]() 与
与![]() 是否垂直,并给出证明过程.
是否垂直,并给出证明过程.
【答案】(1)点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆.
为焦点的椭圆. ![]() (2)
(2)![]() (3)垂直.见解析
(3)垂直.见解析
【解析】
(1)根据题意知![]() ,
,![]() ,所以点
,所以点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆,求出a、b、c即可写出椭圆的方程;(2)当直线斜率不存在时可求得
为焦点的椭圆,求出a、b、c即可写出椭圆的方程;(2)当直线斜率不存在时可求得![]() ,当直线斜率存在时设出直线方程与椭圆方程联立可表示出
,当直线斜率存在时设出直线方程与椭圆方程联立可表示出![]() 、
、![]() ,代入
,代入![]() 中即可求得
中即可求得![]() 的最大值;(3)当有一条切线斜率不存在时求出切线易证两切线垂直;当斜率存在时设出直线方程与椭圆方程联立得到关于x的一元二次方程,由直线与椭圆相切知
的最大值;(3)当有一条切线斜率不存在时求出切线易证两切线垂直;当斜率存在时设出直线方程与椭圆方程联立得到关于x的一元二次方程,由直线与椭圆相切知![]() 即可求出
即可求出![]() ,证明两条切线垂直.
,证明两条切线垂直.
解:(1)由题知:![]() ,
, ![]() ,
,
∴点![]() 的轨迹是以
的轨迹是以![]() 、
、![]() 为焦点的椭圆.
为焦点的椭圆.
由![]() ,得
,得![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴椭圆的标准方程为![]() .
.
(2)当直线![]() 斜率不存在时,直线方程为
斜率不存在时,直线方程为![]() ,则
,则![]() ,
,![]() ,
,
∴![]() .
.
当![]() 斜率存在时,设为
斜率存在时,设为![]() ,直线方程为
,直线方程为![]() ,
,
与![]() 联立,消
联立,消![]() 得
得![]() ,
,
则![]()
![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]()
![]()
![]()
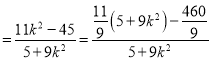
![]() .
.
综上,![]() 的最大值为
的最大值为![]() .
.
(3)垂直.证明如下:设点![]() ,则
,则![]() .
.
①当两切线中有一条切线斜率不存在时,即与![]() 轴垂直时,切线方程为
轴垂直时,切线方程为![]() ,
,
即![]() ,得
,得![]() ,∴另一条切线方程为
,∴另一条切线方程为![]() ,即与
,即与![]() 轴平行,∴两切线垂直.
轴平行,∴两切线垂直.
②当斜率存在时,![]() ,设切线方程为
,设切线方程为![]() ,
,
联立![]() ,消
,消![]() 得
得![]() .
.
由于直线与椭圆相切,得
![]() .
.
化简得![]() .
.
∵![]() ,∴
,∴![]() ,即两条切线相互垂直.
,即两条切线相互垂直.
综上,过点![]() 作的两条切线
作的两条切线![]() 与
与![]() 垂直.
垂直.

练习册系列答案
相关题目