题目内容
本题共有2个小题,每1小题满分6分.已知集合A={x|3x2+x-2≥0,x∈R},B={x|
>0,x∈R}.
(1)用区间表示集合A、B;
(2)求A∩B.
| 4x-3 |
| x-3 |
(1)用区间表示集合A、B;
(2)求A∩B.
(1)A={x|3x2+x-2≥0,x∈R}={x|x≥
或x≤-1}
∵集合B可化为:B={x∈R|(x-3)(4x-3)>0},
∴B={x|x>3或x<
},
所以A=(-∞,-1]∪[
,+∞),B=(-∞,
)∪(3,+∞)(6分)
(2)A∩B={x|x≤-1或
≤x<
或x>3}(12分)
| 2 |
| 3 |
∵集合B可化为:B={x∈R|(x-3)(4x-3)>0},
∴B={x|x>3或x<
| 3 |
| 4 |
所以A=(-∞,-1]∪[
| 2 |
| 3 |
| 3 |
| 4 |
(2)A∩B={x|x≤-1或
| 2 |
| 3 |
| 3 |
| 4 |

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 (本题满分14分)本题共有2个小题,每小题满分各7分.
(本题满分14分)本题共有2个小题,每小题满分各7分.
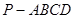 中,底面为直角梯形,
中,底面为直角梯形,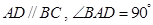 ,
, 垂直于底面
垂直于底面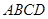 ,
,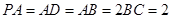 ,
,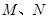 分别为
分别为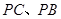 的中点.
的中点.
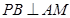 ;
;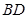 与平面
与平面 所成的角.
所成的角.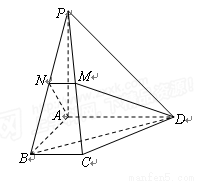
 .
. .
.