题目内容
已知中心在原点,焦点在y轴上的双曲线的离心率为 ,则它的渐近线方程为
,则它的渐近线方程为
- A.y=±2x
- B.y=±
 x
x - C.y=±

- D.

C
分析:可设方程为: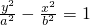 ,由离心率和abc的关系可得b2=2a2,而渐近线方程为y=±
,由离心率和abc的关系可得b2=2a2,而渐近线方程为y=± ,代入可得答案.
,代入可得答案.
解答:由题意可设双曲线的方程为: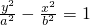 ,
,
则离心率e= =
=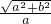 =
= ,即b2=2a2,
,即b2=2a2,
故渐近线方程为y=± =±
=±
故选C
点评:本题考查双曲线的简单性质,涉及的渐近线方程,属基础题.
分析:可设方程为:
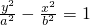 ,由离心率和abc的关系可得b2=2a2,而渐近线方程为y=±
,由离心率和abc的关系可得b2=2a2,而渐近线方程为y=± ,代入可得答案.
,代入可得答案.解答:由题意可设双曲线的方程为:
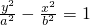 ,
,则离心率e=
 =
=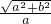 =
= ,即b2=2a2,
,即b2=2a2,故渐近线方程为y=±
 =±
=±
故选C
点评:本题考查双曲线的简单性质,涉及的渐近线方程,属基础题.

练习册系列答案
相关题目