Question

16.如图，在正三棱柱ABC—A₁B₁C₁中，AB=2,AA₁=2.由顶点B沿棱柱侧面经过棱AA₁到顶点C₁的最短路线与AA₁的交点为M.求：

（Ⅰ）三棱柱的侧面展开图的对角线长；

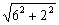
（Ⅱ）该最短路线的长及的值；

（Ⅲ）平面C₁MB与平面ABC所成二面角（锐角）的大小.

Answer 1

16.本小题主要考查直线与平面的位置关系、棱柱等基本知识，考查空间想象能力、逻辑思维能力和运算能力.

  解：（Ⅰ）正三棱ABC－A₁B₁C₁的侧面展开图是长为6，宽为2的矩形，

　　　其对角线长为=2.

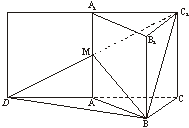
　　（Ⅱ）如图，将侧面AA₁B₁B绕棱AA₁旋转120使其与测面AA₁C₁C在同一平面上，点B运动到点D的位置，连接DC₁交AA₁于M，则DC₁就是由顶点B沿棱柱侧面经过棱AA₁到顶点C₁的最短路线，其长为

　　　　＝＝2.

　　　　∵△DMA≌△C₁MA₁，∴AM＝A₁M，

　　　　故＝1.

　　（Ⅲ）连接DB，C₁B，则DB就是平面C₁MB与平面ABC的交线.

　　　　　在△DCB中，

　　　　　∵∠DBC＝∠CBA+∠ABD＝60+30＝90，

　　　　　∴CB⊥DB，

　　　　　又C₁C⊥平面CBD，

　　　　　由三垂线定理得C₁B⊥DB.

　　　　　∴∠C₁BC就是平面C₁MB与平面ABC所成二面角的平面角（锐角）.

∵侧面C₁B₁BC是正方形,

∴∠C₁BC＝45

故平面C₁MB与平面ABC所成的二面角（锐角）为45.