题目内容
已知向量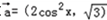 ,
,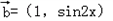 ,函数
,函数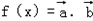 ,
,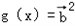 。
。
(1)求函数g(x)的最小正周期;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(c)=3,c=1,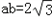 ,且a>b,求a,b的值。
,且a>b,求a,b的值。
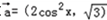 ,
,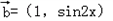 ,函数
,函数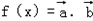 ,
,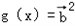 。
。(1)求函数g(x)的最小正周期;
(2)在△ABC中,a,b,c分别是角A,B,C的对边,且f(c)=3,c=1,
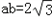 ,且a>b,求a,b的值。
,且a>b,求a,b的值。解:(I)g(x)=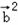 =1+sin22x=1+
=1+sin22x=1+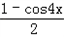 =-
=- cos4x+
cos4x+
∴函数g(x)的最小周期T=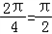 ;
;
(II)f(x)=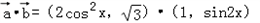 =2
=2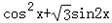
=cos2x+1+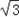 sin2x=2sin(2x+
sin2x=2sin(2x+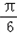 )+1
)+1
f(C)=2sin(2C+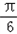 )+1=3
)+1=3
∴sin(2C+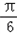 )=1
)=1
∵C是三角形内角
∴2C+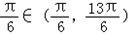 ,
,
∴2C+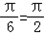
即:C=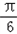
∵cosC=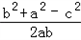 =
=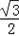
即:a2+b2=7
将ab=2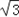 可得:
可得: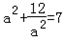
解之得:a2=3或4
∴a=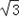 或2
或2
∴b=2或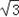 ,
,
∵a>b,
∴a=2,b=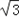 。
。
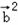 =1+sin22x=1+
=1+sin22x=1+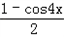 =-
=- cos4x+
cos4x+
∴函数g(x)的最小周期T=
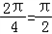 ;
;(II)f(x)=
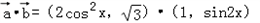 =2
=2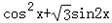
=cos2x+1+
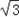 sin2x=2sin(2x+
sin2x=2sin(2x+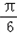 )+1
)+1f(C)=2sin(2C+
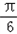 )+1=3
)+1=3∴sin(2C+
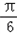 )=1
)=1∵C是三角形内角
∴2C+
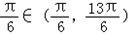 ,
,∴2C+
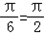
即:C=
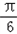
∵cosC=
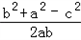 =
=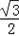
即:a2+b2=7
将ab=2
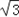 可得:
可得: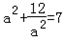
解之得:a2=3或4
∴a=
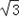 或2
或2∴b=2或
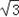 ,
,∵a>b,
∴a=2,b=
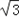 。
。
练习册系列答案
相关题目
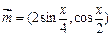 ,
, ,函数
,函数
 的最小正周期;
的最小正周期;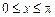 ,求
,求










 ,
, ,函数
,函数 .
. ,
, ,函数
,函数 .
. 在
在 上有解,求
上有解,求 的取值范围;
的取值范围; 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 时,求
时,求 的最小值.
的最小值. ,
, ,函数
,函数 .
. 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间; 时, 求
时, 求 在
在 内的所有实数根之和.
内的所有实数根之和.