题目内容
设函数f(x)=2cos2x+2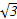
sinxcosx-1(x∈R).
(1)化简函数f(x)的表达式,并求函数f(x)的最小正周期.
(2)若x∈[0,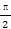
],求函数f(x)的最大值与最小值.
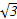sinxcosx-1(x∈R).(1)化简函数f(x)的表达式,并求函数f(x)的最小正周期.
(2)若x∈[0,
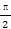],求函数f(x)的最大值与最小值.(1)f(x)=2sin(2x+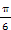
T=π
(2)x=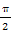
时,f(x)min=-1;x=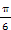时,f(x)max=2.
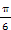T=π(2)x=
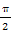时,f(x)min=-1;x=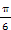时,f(x)max=2.(1)∵f(x)=2cos2x+2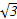sinxcosx-1
=cos2x+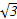sin2x
=2sin(2x+),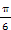
∴函数f(x)的最小正周期T=π.
(2)∵0≤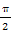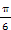x≤,∴≤2x+≤
,
∴-
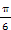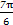≤sin(2x+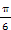)≤1,
∴-1≤2sin(2x+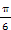)≤2,
∴当2x+=,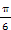
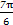即x=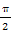时,f(x)min=-1;
当2x+=,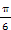
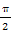即x=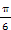时,f(x)max=2.
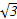sinxcosx-1=cos2x+
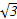sin2x=2sin(2x+
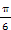),∴函数f(x)的最小正周期T=π.
(2)∵0≤x≤
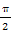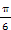,∴≤2x+≤,∴-
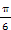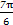≤sin(2x+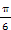)≤1,∴-1≤2sin(2x+
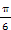)≤2,∴当2x+
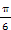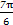=,即x=
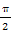时,f(x)min=-1;当2x+
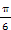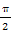=,即x=
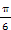时,f(x)max=2.
练习册系列答案
快捷英语周周练系列答案
相关题目
.
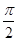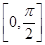上的最大值和最小值．
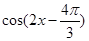＋2cos2x.
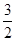，b＋c＝2，求a的最小值．
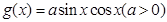的最大值为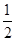
，则函数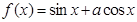
的图象的一条对称轴方程为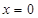
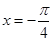
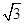cos x＋sin x(x∈R)的图象向左平移m(m＞0)个单位长度后，所得到的图象关于y轴对称，则m的最小值是( )
sin2x+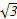
cos2x-
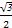的最小正周期等于( )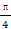
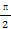
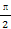),则ω= ,φ= .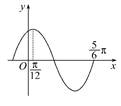
cos2x+
)(k∈Z)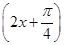
的最小正周期为 ________.