题目内容
设y=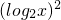 +(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,则x的取值范围是________.
+(t-2)log2x-t+1,若t在[-2,2]上变化时,y恒取正值,则x的取值范围是________.
(0, )∪(8,+∞)
)∪(8,+∞)
分析:构造函数f(t)=(log2x-1)t+(log2x)2-2log2x+1,根据t∈[-2,2]时,f(t)恒为正值,可得f(-2)>0,f(2)>0,即可得到不等式,由此可确定x的取值范围.
解答:构造函数f(t)=(log2x-1)t+(log2x)2-2log2x+1,
∵t∈[-2,2]时,f(t)恒为正值,
∴f(-2)>0,f(2)>0
∴-2(log2x-1)+(log2x)2-2log2x+1>0,2(log2x-1)+(log2x)2-2log2x+1>0
∴(log2x)2-4log2x+3>0,(log2x)2-1>0
∴log2x<-1或log2x>3,
即0<x< 或x>8.
或x>8.
故答案为:(0, )∪(8,+∞)
)∪(8,+∞)
点评:本题考查复合函数的单调性,解题的关键是变换主元,构建新函数,属于中档题.
 )∪(8,+∞)
)∪(8,+∞)分析:构造函数f(t)=(log2x-1)t+(log2x)2-2log2x+1,根据t∈[-2,2]时,f(t)恒为正值,可得f(-2)>0,f(2)>0,即可得到不等式,由此可确定x的取值范围.
解答:构造函数f(t)=(log2x-1)t+(log2x)2-2log2x+1,
∵t∈[-2,2]时,f(t)恒为正值,
∴f(-2)>0,f(2)>0
∴-2(log2x-1)+(log2x)2-2log2x+1>0,2(log2x-1)+(log2x)2-2log2x+1>0
∴(log2x)2-4log2x+3>0,(log2x)2-1>0
∴log2x<-1或log2x>3,
即0<x<
 或x>8.
或x>8.故答案为:(0,
 )∪(8,+∞)
)∪(8,+∞)点评:本题考查复合函数的单调性,解题的关键是变换主元,构建新函数,属于中档题.

练习册系列答案
相关题目
 已知双曲线
已知双曲线 (2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为
(2013•揭阳二模)如图已知抛物线C:y2=2px(p>0)的准线为l,焦点为F,圆M的圆心在x轴的正半轴上,且与y轴相切.过原点作倾斜角为