Question

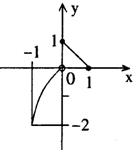（2008•和平区三模）已知函数y=f（x）的定义域为[-1，1]，其图象如图所示，则不等式-1≤f^-1（x）≤

1

2

的解集为（　　）

• A．[-1，

  1

  2

  ]
• B．[-2，

  1

  2

  ]
• C．[-2，0)∪[

  1

  2

  ，1]
• D．[-1，0)∪(

  1

  2

  ，1]

Answer 1

分析：求-1≤f^-1（x）≤

1

2

的解集，即求-1≤f（x）≤

1

2

时，x的取值范围，根据已知中图象可得答案．

解答：解：求-1≤f^-1（x）≤

1

2

的解集
即求-1≤f（x）≤

1

2

时，x的取值范围
∵f（x）=

1

2

时，x=

1

2

，f（x）=0时，x=0
∴当-1≤f（x）＜0时，x∈[-2，0）
当0≤f（x）≤

1

2

时，x∈[

1

2

，1]
∴当-1≤f（x）≤

1

2

时，x∈[-2，0)∪[

1

2

，1]
故选C

点评：本题考查的知识点是反函数，函数的图象，函数与不等式的综合应用，其中利用转化思想，将求-1≤f^-1（x）≤

1

2

的解集，转化为求-1≤f（x）≤

1

2

时，x的取值范围，是解答的关键．