题目内容
已知函数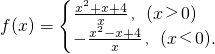
(1)求证:函数f(x)是偶函数;
(2)判断并证明函数f(x)在区间(0,2]上的单调性;
(3)根据以上结论猜测f(x)在[-2,0)上的单调性,不需要证明.
解:(1)当x>0时,-x<0,则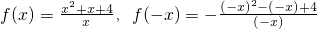 =
= ,
,
∴f(x)=f(-x).
当x<0时,-x>0,则 =
=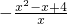 ,
,
∴f(x)=f(-x).
综上所述,对于x≠0,都有f(x)=f(-x),∴函数f(x)是偶函数.
(2)当x>0时,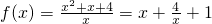 ,
,
设x2>x1>0,则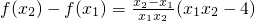 .
.
当2≥x2>x1>0时,f(x2)-f(x1)<0,∴函数f(x)在(0,2]上是减函数.
(3)根据偶函数的图象的对称性可得,函数为增函数.
分析:(1)当x>0时,-x<0,证明f(x)=f(-x);当x<0时,-x>0,证明f(x)=f(-x),可得对于x≠0,
都有f(x)=f(-x),故 函数f(x)是偶函数.
(2)设x2>x1>0,则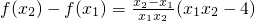 ,当2≥x2>x1>0时,f(x2)-f(x1)<0,
,当2≥x2>x1>0时,f(x2)-f(x1)<0,
故函数f(x)在(0,2]上是减函数.
(3)根据偶函数的图象的对称性可得,函数为增函数.
点评:本题考查证明函数的奇偶性的方法,以及证明函数的单调性的证明方法,偶函数的图象的对称性,明函数的奇偶性
是解题的难点.
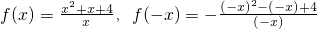 =
= ,
,∴f(x)=f(-x).
当x<0时,-x>0,则
 =
=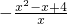 ,
,∴f(x)=f(-x).
综上所述,对于x≠0,都有f(x)=f(-x),∴函数f(x)是偶函数.
(2)当x>0时,
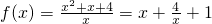 ,
,设x2>x1>0,则
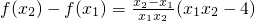 .
.当2≥x2>x1>0时,f(x2)-f(x1)<0,∴函数f(x)在(0,2]上是减函数.
(3)根据偶函数的图象的对称性可得,函数为增函数.
分析:(1)当x>0时,-x<0,证明f(x)=f(-x);当x<0时,-x>0,证明f(x)=f(-x),可得对于x≠0,
都有f(x)=f(-x),故 函数f(x)是偶函数.
(2)设x2>x1>0,则
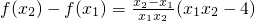 ,当2≥x2>x1>0时,f(x2)-f(x1)<0,
,当2≥x2>x1>0时,f(x2)-f(x1)<0,故函数f(x)在(0,2]上是减函数.
(3)根据偶函数的图象的对称性可得,函数为增函数.
点评:本题考查证明函数的奇偶性的方法,以及证明函数的单调性的证明方法,偶函数的图象的对称性,明函数的奇偶性
是解题的难点.

练习册系列答案
相关题目
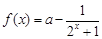 .
.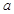 为何实数
为何实数 总是为增函数;(2)确定
总是为增函数;(2)确定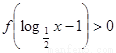
 .
.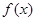 在点
在点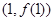 处的切线恒过定点,并求出定点坐标;
处的切线恒过定点,并求出定点坐标;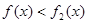 在区间
在区间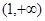 上恒成立,求
上恒成立,求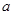 的取值范围;
的取值范围;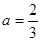 时,求证:在区间
时,求证:在区间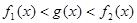 恒成立的函数
恒成立的函数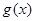
 .
. 为何实数
为何实数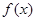 总是为增函数;
总是为增函数;