Question

已知中心在原点，焦点在坐标轴上的椭圆Ω，它的离心率为，一个焦点和抛物线y²=-4x的焦点重合，过直线l：x=4上一点M引椭圆Ω的两条切线，切点分别是A，B．
（Ⅰ）求椭圆Ω的方程；
（Ⅱ）若在椭圆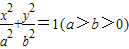上的点（x，y）处的椭圆的切线方程是．求证：直线AB恒过定点C；并出求定点C的坐标．
（Ⅲ）是否存在实数λ，使得|AC|+|BC|=λ|AC|•|BC|恒成立？（点C为直线AB恒过的定点）若存在，求出λ的值；若不存在，请说明理由．

Answer 1

【答案】分析：（Ⅰ）设椭圆方程为，根据它的一个焦点和抛物线y²=-4x的焦点重合，从而求出c值，再求出a和b的值，从而求解；
（Ⅱ）切点坐标为A（x₁，y₁），B（x₂，y₂），直线l上一点M的坐标（4，t），求出切线方程，再把点M代入切线方程，说明点A，B的坐标都适合方程，而两点之间确定唯一的一条直线，从而求出定点；
（Ⅲ）联立直线方程和椭圆的方程进行联立，求出两根的积和两根的和，求出|AC|，|BC|的长，求出λ的值看在不在，再进行判断；
解答：解：（I）设椭圆方程为．
抛物线y²=-4x的焦点是（-1，0），故c=1，又，
所以，
所以所求的椭圆Ω方程为…（4分）
（II）设切点坐标为A（x₁，y₁），B（x₂，y₂），
直线l上一点M的坐标（4，t）．
则切线方程分别为，．
又两切线均过点M，
即，
即点A，B的坐标都适合方程，而两点之间确定唯一的一条直线，
故直线AB的方程是，显然对任意实数t，点（1，0）都适合这个方程，
故直线AB恒过定点C（1，0）．           …（9分）
（III）将直线AB的方程，代入椭圆方程，
得，即
所以
不妨设y₁＞0，y₂＜0，
同理…（12分）
所以=
即．
故存在实数，使得|AC|+|BC|=λ|AC|•|BC|．   …（15分）
点评：此题主要考查利用导数研究函数的切线方程，第三问是一个存在性问题，利用了根与系数的关系，需要联立方程，考查了学生的计算能力，是一道难题；