题目内容
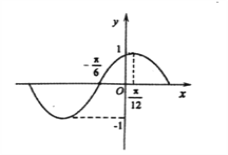
【题目】函数
的部分图像如图所示，将
的图象向右平移
个单位长度后得到函数
的图象.
（1）求函数
的解析式；
（2）在
中，角A,B,C满足
，且其外接圆的半径R=2，求
的面积的最大值.
【答案】（1）
（2）
【解析】试题分析：（1）由图知周期
，利用周期公式可求
，由
，结合范围
，可求
的值，进而利用三角函数图象变换的规律即可得解；（2）利用三角函数恒等变换的应用及三角形内角和定理化简已知可得
，进而可求
，由正弦定理解得
的值，进而由余弦定理，基本不等式可求
，利用三角形面积公式即可得解面积的最大值.
试题解析：（1）由图知， 
，解得： 
，
，∴
，即
，
∵
，∴
.
∴
，
即函数
的解析式
.
（2）∵
，∴
，
， 
， 
，
或1（舍），
，
由正弦定理得： 
， 
，
由余弦定理得： 
， 
，
，
∴
的面积最大值为
.
练习册系列答案
相关题目
