题目内容
表达式sin（45°+A）-sin（45°-A）化简后为（ ）A．-
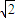sinAB．
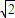sinAC．
sinAD．-
sinA
【答案】分析：利用两角和与差的正弦函数把sin（45°+A）-sin（45°-A）等价转化为sin45°cosA+cos45°sinA-sin45°cosA+cos45°sinA，由此能求出结果．
解答：解：sin（45°+A）-sin（45°-A）
=sin45°cosA+cos45°sinA-sin45°cosA+cos45°sinA
=2cos45°sinA
=
sinA．
故选B．
点评：本题考查两角和与差的正弦函数的应用，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
解答：解：sin（45°+A）-sin（45°-A）
=sin45°cosA+cos45°sinA-sin45°cosA+cos45°sinA
=2cos45°sinA
=
sinA．故选B．
点评：本题考查两角和与差的正弦函数的应用，解题时要认真审题，仔细解答，注意等价转化思想的合理运用．
练习册系列答案
暑假作业海燕出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
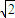sinA
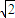sinA
sinA
sinA