题目内容
求证:以过抛物线 焦点的弦为直径的圆必与
焦点的弦为直径的圆必与 相切(用分析法证)
相切(用分析法证)
【答案】
见解析。
【解析】
试题分析:
证明:(如图) 过焦点
过焦点 ,作
,作 垂直准线,取
垂直准线,取 的中点
的中点 ,作
,作 垂直准线.
垂直准线.

要证明以 为直径的圆与准线相切,
为直径的圆与准线相切,
只需证 ,
,
由抛物线的定义: ,
, ,
,
所以 ,
,
因此只需证 .
.
根据梯形的中位线定理可知上式是成立的.
所以,以过焦点的弦为直径的圆必与 相切.
相切.
考点:本题主要考查分析法的定义和方法、抛物线定义。
点评:数形结合,综合应用解析几何知识。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的焦点F的直线
的焦点F的直线 与抛物线相交于A,B两点。
与抛物线相交于A,B两点。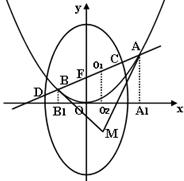
 的交点为C、D,是否存在直线
的交点为C、D,是否存在直线 ,若存在,求出直线
,若存在,求出直线