题目内容
已知f(x)= sinxcosx-cos2x-
sinxcosx-cos2x- .
.
(1)求函数f(x)的最小正周期,单调增区间.
(2)设△ABC的三内角A,B,C对边分别为a,b,c且c= ,f(C)=0,若
,f(C)=0,若 =(1,sinA),
=(1,sinA), =(2,sinB)共线,求a,b的值.
=(2,sinB)共线,求a,b的值.
解:(1)f(x)= sinxcosx-cos2x-
sinxcosx-cos2x- =
=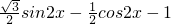 =sin(2x-
=sin(2x- )-1
)-1
∴函数f(x)的最小正周期T=π.
2kπ ?
?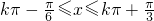 k∈Z
k∈Z
所以单调增区间: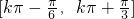 k∈Z
k∈Z
(2)∵f(x)=sin(2x- )-1,f(C)=0
)-1,f(C)=0
∴f(C)=sin(2C- )-1=0,C为三角形内角,所以C=
)-1=0,C为三角形内角,所以C= .
.
 =(1,sinA),与
=(1,sinA),与 =(2,sinB)共线,所以sinB=2sinA?b=2a…①
=(2,sinB)共线,所以sinB=2sinA?b=2a…①
由余弦定理得:c2=a2+b2-2abcosC即c2=a2+b2-ab…②
由①②得a=1,b=2
分析:(1)化简函数的表达式为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期,利用正弦函数的单调增区间求出函数的单调增区间.
(2)通过函数的表达式以及f(C)=0,求出C 的值,利用 =(1,sinA),
=(1,sinA), =(2,sinB)共线,和余弦定理求出a,b的值.
=(2,sinB)共线,和余弦定理求出a,b的值.
点评:本题是基础题,考查三角函数的化简求值,三角函数的周期的求法,余弦定理的应用,向量的应用,考查计算能力,常考题型.
 sinxcosx-cos2x-
sinxcosx-cos2x- =
=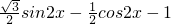 =sin(2x-
=sin(2x- )-1
)-1∴函数f(x)的最小正周期T=π.
2kπ
 ?
?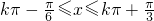 k∈Z
k∈Z所以单调增区间:
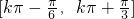 k∈Z
k∈Z(2)∵f(x)=sin(2x-
 )-1,f(C)=0
)-1,f(C)=0∴f(C)=sin(2C-
 )-1=0,C为三角形内角,所以C=
)-1=0,C为三角形内角,所以C= .
. =(1,sinA),与
=(1,sinA),与 =(2,sinB)共线,所以sinB=2sinA?b=2a…①
=(2,sinB)共线,所以sinB=2sinA?b=2a…①由余弦定理得:c2=a2+b2-2abcosC即c2=a2+b2-ab…②
由①②得a=1,b=2
分析:(1)化简函数的表达式为一个角的一个三角函数的形式,然后求函数f(x)的最小正周期,利用正弦函数的单调增区间求出函数的单调增区间.
(2)通过函数的表达式以及f(C)=0,求出C 的值,利用
 =(1,sinA),
=(1,sinA), =(2,sinB)共线,和余弦定理求出a,b的值.
=(2,sinB)共线,和余弦定理求出a,b的值.点评:本题是基础题,考查三角函数的化简求值,三角函数的周期的求法,余弦定理的应用,向量的应用,考查计算能力,常考题型.

练习册系列答案
相关题目
已知f(x)=sin(x+
),g(x)=cos(x-
),则f(x)的图象( )
| π |
| 2 |
| π |
| 2 |
| A、与g(x)的图象相同 | ||
| B、与g(x)的图象关于y轴对称 | ||
C、向左平移
| ||
D、向右平移
|