Question

【题目】[2018·沧州质检]对于椭圆，有如下性质：若点是椭圆上的点，则椭圆在该点处的切线方程为．利用此结论解答下列问题．点是椭圆上的点，并且椭圆在点处的切线斜率为．

（1）求椭圆的标准方程；

（2）若动点在直线上，经过点的直线，与椭圆相切，切点分别为，．求证：直线必经过一定点．

Answer 1

【答案】（1）（2）直线必经过一定点

【解析】试题分析：

(Ⅰ)由题意结合所给的知识可得椭圆在点处的切线斜率为，则.且.据此解方程组可得椭圆的方程为；

(Ⅱ)设，，，切线，切线.由两条切线都经过同一点可得直线的方程为.据此整理计算有.求解方程组可得直线必经过一定点.

试题解析：

（Ⅰ）∵椭圆在点处的切线方程为，

其斜率为，

∴.

又点在椭圆上，

∴.

解得，.

∴椭圆的方程为；

（Ⅱ）设，，，

则切线，切线.

∵都经过点，

∴，.

即直线的方程为.

又，

∴，

即.

令得

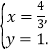
∴直线必经过一定点.