Question

已知a为实数，函数f（x）=（1+ax）e^x，函数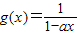，令函数F（x）=f（x）•g（x）．
（1）若a=1，求函数f（x）的极小值；
（2）当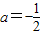时，解不等式F（x）＜1；
（3）当a＜0时，求函数F（x）的单调区间．

Answer 1

【答案】分析：（1）a=1代入f（x），对其进行求导，得到极值点，利用导数研究函数的单调性问题；
（2）把a=- 代入f（x）和g（x），从而得到F（x），再代入不等式F（x）＜1进行求解；
（3）求导数F′（x），在定义域内解不等式F′（x）＞0，F^′（x）＜0，分a，a=，-a＜0，三种情况进行讨论即可解得，由导数与函数单调性关系即得单调区间
解答：（1）由f'（x）=e^x+（1+x）e^x=0得x=-2，
当x＜-2时，f'（x）＜0，f（x）在（-∞，-2）上单调递减，
当x＞-2时，f'（x）＞0，f（x）在（-2，+∞）上单调递增，
所以函数f（x）的最小值为f（-2）=-e^-2；
（2）当a=-时F（x）=＜1，即
设m（x）=，则m（0）=0，＜0
所以m（x）的单调递减区间是（-∞，-2）和（-2，+∞），
而当x＜-2时，总有成立，
所以不等式F（x）＜1的解集是（-∞，-2）∪（0，+∞）．
（3），定义域为{x|}
则=，令F′（x）=0，得（a＜0）
①当2a+1＜0，即时，F′（x）＜0
则当时，函数F（x）的单调递减区间是（-∞，）和（，+∞）．
②当2a+1=0，即时，由（2）知，函数F（x）的单调递减区间是（-∞，-2）和（-2，+∞）．
③当2a+1＞0，即时，解得到，
∵，∴令F′（x）＜0，得到x∈（-∞，），x∈（，），x∈；
令F′（x）＞0，得到x∈（，）．
则当时，函数F（x）的单调递减区间是（-∞，），（，），；
函数F（x）的单调递增区间是（，）．
点评：此题主要考查利用导数研究函数单调性问题，考查分类讨论思想，属中档题．