题目内容
已知向量a="(cos" α,sin α),b="(cos" β,sin β),0<β<α<π.
(1)若|a-b|=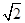 ,求证:a⊥b;
,求证:a⊥b;
(2)设c=(0,1),若a+b=c,求α,β的值.
(1)见解析 (2) α= ,β=
,β=
解析(1)证明:由|a-b|=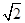 得
得
(cosα-cos β)2+(sinα-sinβ)2=2,
即2-2cosαcosβ-2sinαsinβ=2,
∴cosαcosβ+sinαsinβ=0,
即a·b=0,
∴a⊥b.
(2)解:因为a+b=(cosα+cosβ,sin α+sinβ)=(0,1),
所以
由此得,cosα=cos(π-β),
由0<β<π,得0<π-β<π.
又0<α<π,
故α=π-β.
代入sinα+sinβ=1,得sinα=sinβ= ,
,
而α>β,
所以α= ,β=
,β= .
.

练习册系列答案
相关题目
在数列1,1,2,3,5,8, ,21,34,55,…中,
,21,34,55,…中, 等于( )
等于( )
| A.11 | B.12 | C.13 | D.14 |
 是已知平面
是已知平面 上所有向量的集合,对于映射
上所有向量的集合,对于映射 ,记
,记 的象为
的象为 。若映射
。若映射 满足:对所有
满足:对所有 及任意实数
及任意实数 都有
都有 ,则
,则 称为平面
称为平面 ;
; 是平面
是平面 ,则
,则 ,则
,则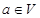 ,则对任意实数
,则对任意实数 均有
均有 。
。 =(cos
=(cos ,cos(
,cos( ),
), =(
=( ,sin
,sin
 的值;
的值; ,求
,求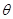 ;
; ,求证:
,求证: .
.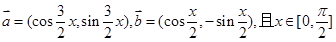 ,
,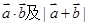 ;
;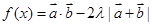 的最小值是
的最小值是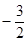 ,求实数
,求实数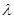 的值.
的值.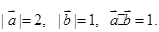
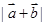 的值; (2)若
的值; (2)若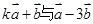 垂直,求
垂直,求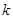 的值.
的值. ,
, ,当
,当 为何值时,
为何值时, 与
与 垂直?(2)
垂直?(2)
 与
与
 =
= +λ·
+λ· (λ∈R),试问:
(λ∈R),试问: .
. ,求
,求 ;
; 的最大值.
的最大值.