题目内容
设 是定义在
是定义在 上的函数,当
上的函数,当 ,且
,且 时,有
时,有 .
.
(1)证明 是奇函数;
是奇函数;
(2)当 时,
时, (a为实数). 则当
(a为实数). 则当 时,求
时,求 的解析式;
的解析式;
(3)在(2)的条件下,当 时,试判断
时,试判断 在
在 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
【答案】
(1)函数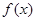 定义域对称
定义域对称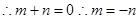
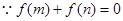
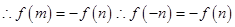 即
即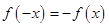 ,函数
,函数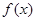 是奇函数
是奇函数
(2)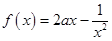 (3)
(3)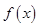 在
在 上是增函数
上是增函数
【解析】
试题分析:(1)函数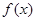 定义域对称
定义域对称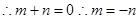
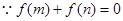
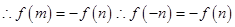 即
即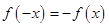 ,函数
,函数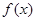 是奇函数
是奇函数
(2)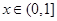 时
时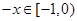
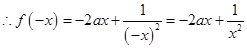
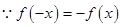
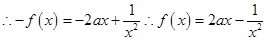
(3)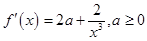 时
时 恒成立,
恒成立,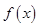 在
在 上是增函数,
上是增函数,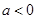 时,令
时,令 得
得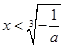 ,
,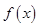 在
在 上是增函数,综上当
上是增函数,综上当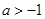 时
时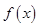 在
在 上是增函数
上是增函数
考点:求函数解析式及函数性质
点评:判断函数奇偶性需在定义域对称的条件下判断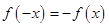 ,
,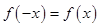 哪一个成立,判断函数单调性,只需判定导数大于零还是小于零
哪一个成立,判断函数单调性,只需判定导数大于零还是小于零

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 是定义在
是定义在 上的函数,且
上的函数,且 ,当
,当 时,
时, ,那么当
,那么当 时,
时, 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 上的3级类增函数
上的3级类增函数 上的1级类增函数
上的1级类增函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。 是定义在
是定义在 上的函数,且对任意
上的函数,且对任意 ,当
,当 时,都有
时,都有 ;
; 时,比较
时,比较 的大小;
的大小; ;
; 且
且 ,求
,求 的取值范围。
的取值范围。