Question

设是定义在上的函数，若存在，使得在上单调递增，在上单调递减，则称为上的单峰函数，为峰点，包含峰点的区间为含峰区间.　　对任意的上的单峰函数，下面研究缩短其含峰区间长度的方法.

  （1）证明：对任意的，，若，则为含峰区间；若，则为含峰区间；

  （2）对给定的，证明：存在，满足，使得由（1）所确定的含峰区间的长度不大于；

Answer 1

证明见解析

解析:

(1)证明:设为的峰点,则由单峰函数定义可知, 在上单调递增, 在上单调递减,

当时,假设,则<,从而这与矛盾,所以,即为含峰区间.

当时,假设,则,从而这与矛盾,所以,即为含峰区间………………………….(7分)

  （2）证明：由(1)的结论可知:

当时, 含峰区间的长度为；

当时, 含峰区间的长度为；

对于上述两种情况，由题意得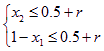               ①

由①得即，

又因为，所以                     ②

将②代入①得                    ③

由①和③解得

所以这时含峰区间的长度，

即存在使得所确定的含峰区间的长度不大于