题目内容
(2012•宣城模拟)已知三次函数f(x)=ax3+bx2+cx+d(a≠0)为R上奇函数,且在x=
处取得极值-
.记函数图象为曲线C.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设曲线C与其在点P1(1,f(1))处的切线交于另一点P2(x2,f(x2)),线段P1P2与曲线C所围成封闭图形的面积记为S1,求S1的值;
(Ⅲ) 在(Ⅱ)的条件下,设曲线C与其在点P2处的切线交于另一点P3(x3,f(x3)),线段P2P3与曲线C所围成封闭图形的面积记为S2,…,按此方法依次做下去,即设曲线C与其在点Pn(xn,f(xn))处的切线交于另一点Pn+1(xn+1,f(xn+1)),线段PnPn+1与曲线C所围成封闭图形的面积记为Sn,试求Sn关于n的表达式.
| ||
| 3 |
2
| ||
| 9 |
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设曲线C与其在点P1(1,f(1))处的切线交于另一点P2(x2,f(x2)),线段P1P2与曲线C所围成封闭图形的面积记为S1,求S1的值;
(Ⅲ) 在(Ⅱ)的条件下,设曲线C与其在点P2处的切线交于另一点P3(x3,f(x3)),线段P2P3与曲线C所围成封闭图形的面积记为S2,…,按此方法依次做下去,即设曲线C与其在点Pn(xn,f(xn))处的切线交于另一点Pn+1(xn+1,f(xn+1)),线段PnPn+1与曲线C所围成封闭图形的面积记为Sn,试求Sn关于n的表达式.
分析:(I)利用奇函数的特点,采用特殊值代入法即可解得b=d=0,再利用函数极值的特点,列方程组即可解得a、c的值,从而确定函数的解析式;
(II)先利用导数的几何意义,计算曲线C与其在点P1(1,f(1))处的切线方程,再利用定积分的几何意义,通过求定积分计算线段P1P2与曲线C所围成封闭图形的面积
(III)先利用导数的几何意义,计算曲线C与其在点Pn(xn,f(xn))处的切线方程,再利用定积分的几何意义,通过求定积分计算线段PnPn+1与曲线C所围成封闭图形的面积Sn,发现数列{Sn}为等比数列,从而利用等比数列的通项公式计算Sn关于n的表达式即可
(II)先利用导数的几何意义,计算曲线C与其在点P1(1,f(1))处的切线方程,再利用定积分的几何意义,通过求定积分计算线段P1P2与曲线C所围成封闭图形的面积
(III)先利用导数的几何意义,计算曲线C与其在点Pn(xn,f(xn))处的切线方程,再利用定积分的几何意义,通过求定积分计算线段PnPn+1与曲线C所围成封闭图形的面积Sn,发现数列{Sn}为等比数列,从而利用等比数列的通项公式计算Sn关于n的表达式即可
解答:解:(Ⅰ)∵三次函数为R上奇函数,∴f(0)=0,f(-1)=-f(1)
即d=0且-a+b-c=-a-b-c
∴b=d=0
即f(x)=ax3+cx,f′(x)=3ax2+c,又f(x)=ax3+cx在x=
处取得极值-
,
∴
即
得a=1,c=-1,∴f(x)=x3-x
(Ⅱ)∵f′(x)=3x2-1,f(1)=0,f′(1)=2,
∴曲线C在点P1处的切线方程为y=2(x-1)
由
解得x1=1,x2=-2,
∴S1=|
x3-x-2(x-1)dx|=|(
x4 -
x2+2x)
|=
(Ⅲ)f(x)在Pn(xn,f(xn))的切线:
y-(xn3-xn)=(3xn2-1)(x-xn)即y=(3xn2-1)x-2xn3
由
解得x=xn或x=-2xn,
∴Pn+1(-2xn,f(-2xn)),xn+1=-2xn,
Sn=|
x3-x-[(3xn2-1)x-2xn3]dx|=|(
x4 -
xn2x2+2xn3x)
|=
xn4
同理得Sn+1=
xn+14,又xn+1=-2xn≠0,∴
=(
)4=16,又S1=
∴Sn=
•16n-1=
•16n n∈N*.
即d=0且-a+b-c=-a-b-c
∴b=d=0
即f(x)=ax3+cx,f′(x)=3ax2+c,又f(x)=ax3+cx在x=
| ||
| 3 |
2
| ||
| 9 |
∴
|
|
得a=1,c=-1,∴f(x)=x3-x
(Ⅱ)∵f′(x)=3x2-1,f(1)=0,f′(1)=2,
∴曲线C在点P1处的切线方程为y=2(x-1)
由
|
∴S1=|
| ∫ | 1 -2 |
| 1 |
| 4 |
| 3 |
| 2 |
| | | 1 -2 |
| 27 |
| 4 |
(Ⅲ)f(x)在Pn(xn,f(xn))的切线:
y-(xn3-xn)=(3xn2-1)(x-xn)即y=(3xn2-1)x-2xn3
由
|
∴Pn+1(-2xn,f(-2xn)),xn+1=-2xn,
Sn=|
| ∫ | -2xn xn |
| 1 |
| 4 |
| 3 |
| 2 |
| | | -2xn xn |
| 27 |
| 4 |
同理得Sn+1=
| 27 |
| 4 |
| Sn+1 |
| Sn |
| xn+1 |
| xn |
| 27 |
| 4 |
∴Sn=
| 27 |
| 4 |
| 27 |
| 64 |
点评:本题综合考查了函数的性质,导数的几何意义,导数在函数极值中的应用,定积分的几何意义及其运算,函数与数列的综合运用,等比数列的通项公式等知识,综合性较强,难度较大

练习册系列答案
相关题目
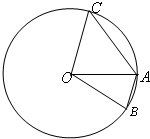 (2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则
(2012•宣城模拟)如图,⊙O的半径为1,点A,B,C是⊙O上的点,且∠AOB=30°,AC=2AB,则