Question

已知z是复数,z+2i,均为实数(i为虚数单位)且复数(z+xi)²在复平面上对应的点在第一象限内.

求实数x的取值范围.

Answer 1

分析:要判定z+2i和为实数,需先将z设出用a+bi表示(a、b∈R),再通过四则运算判定.

解:设z=a+bi(a、b∈R),

则z+2i=a+bi+2i=a+(b+2)i为实数.

∴b=-2.

∴z=a-2i.

∵

=

=为实数,

∴a=4.∴z=4-2i.

又∵(z+xi)²=(4-2i+xi)²

=［4+(x-2)i］²

=16+8(x-2)i-(x-2)²

=-x²+4x+12+8(x-2)i,

∵(z+xi)²在复平面内对应的点在第一象限内,

∴

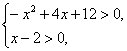
即2＜x＜6.

∴实数x的取值范围为(2,6).

绿色通道

    本题综合了实数的概念、复数的四则运算及复数的几何意义.要熟练掌握复数的四则运算.