题目内容
(本题12分)
设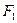 、
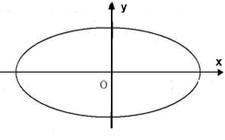
、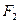 分别是椭圆
分别是椭圆 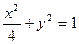 的左、右焦点,
的左、右焦点,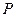 是该椭圆上的一个动点,
是该椭圆上的一个动点, 为坐标原点.
为坐标原点.
(1)求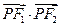 的取值范围;
的取值范围;
(2)设过定点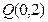 的直线
的直线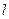 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠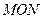 为锐角,求直线
为锐角,求直线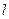 的斜率
的斜率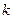 的取值范围
的取值范围 .
.
设
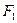 、
、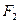 分别是椭圆
分别是椭圆 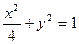 的左、右焦点,
的左、右焦点,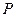 是该椭圆上的一个动点,
是该椭圆上的一个动点, 为坐标原点.
为坐标原点. 
(1)求
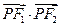 的取值范围;
的取值范围; (2)设过定点
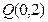 的直线
的直线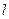 与椭圆交于不同的两点M、N,且∠
与椭圆交于不同的两点M、N,且∠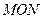 为锐角,求直线
为锐角,求直线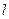 的斜率
的斜率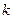 的取值范围
的取值范围 .
.

所以
 的值范围为[-2,1] ……………5分
的值范围为[-2,1] ……………5分(2)设直线l的方程为y=kx+2,代入椭圆方程
 得(2k2+1)x2+16kx+12,因为直线l与椭圆交于不同的两点,所以Δ=(16k2)-4·12·(4k2+1)=16·(4k2-3)>0,
得(2k2+1)x2+16kx+12,因为直线l与椭圆交于不同的两点,所以Δ=(16k2)-4·12·(4k2+1)=16·(4k2-3)>0,

 取值范围为
取值范围为 ∪
∪

略

练习册系列答案
相关题目
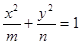 的离心率为_______________
的离心率为_______________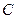 的中心在原点,焦点在
的中心在原点,焦点在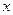 轴上,离心率为
轴上,离心率为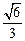 ,并与直线
,并与直线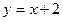 相切.
相切.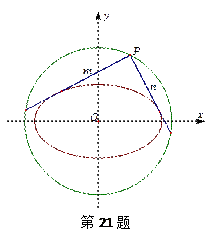
 :
: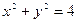 上任意一点
上任意一点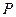 作椭圆
作椭圆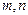 . 求证:
. 求证: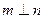 .
.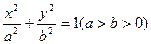 的短轴长为
的短轴长为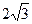 ,右焦点
,右焦点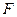 与抛物线
与抛物线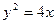 的焦点重合,
的焦点重合, 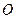 为坐标原点
为坐标原点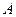 、
、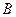 是椭圆C上的不同两点,点
是椭圆C上的不同两点,点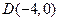 ,且满足
,且满足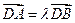 ,若
,若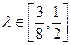 ,求直线AB的斜率的取值范围.
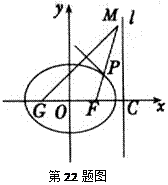
,求直线AB的斜率的取值范围.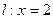 ,设动点P到直线
,设动点P到直线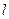 的距离为
的距离为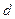 ,已知
,已知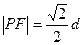 ,且
,且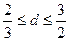 .
.
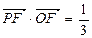 ,求向量
,求向量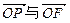 的夹角;
的夹角;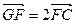 ,点M满足
,点M满足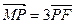 ,且线段MG的垂直平分线经过点P,求
,且线段MG的垂直平分线经过点P,求 的面积.
的面积.
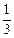 .
. )过椭圆左顶点作直线l垂直于x轴
)过椭圆左顶点作直线l垂直于x轴 ,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求点M的轨迹方程.
,若动点M到椭圆右焦点的距离比它到直线l的距离小4,求点M的轨迹方程.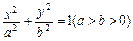 短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .
短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .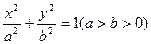 的离心率为
的离心率为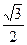 ,那么双曲线
,那么双曲线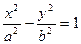 的离心率是 ( )
的离心率是 ( )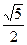
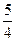
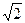
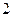
 的
的 左焦点为F,右顶点为A,点B在椭圆上,且
左焦点为F,右顶点为A,点B在椭圆上,且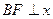 轴,直线AB交
轴,直线AB交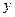 轴于点P。若
轴于点P。若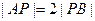 ,则椭圆的离心率为
,则椭圆的离心率为