题目内容
如图,P是△ABC所在平面外一点,A′、B′、C′分别是△PBC、△PAC、△PAB的重心.
(1)求证:平面A′B′C′∥平面ABC;
(2)求△A′B′C′与△ABC的面积之比.
分析:(1)欲证结论成立,需证明面A′B′C′内两条相交直线A′B′、A′C′都与面ABC平行即可.
如要证A′C′∥面ABC,只需证A′C′∥MN,而由三角形重心的性质易得A′C′∥MN.
(2)求出△A′B′C′与△ABC的相似性.
(1)证明:连结PA′、PC′,并延长交BC、AB于N、M两点,连结MN.
∵A′、C′分别是△PBC、△PAB的重心,
∴PA′=![]() PN,PC′=
PN,PC′=![]() PM.
PM.
∴A′C′![]()
![]() MN.
MN.
∴A′C′∥平面ABC.
同理,A′B′∥平面ABC.
又A′C′∩A′B′=A′,
∴平面A′B′C′∥平面ABC.
(2)解:由(1)知A′C′=![]() MN=
MN=![]() AC,
AC,
∴S△A′B′C′∶S△ABC=![]() .
.
点评:平面几何中的几何性质(如本题重心)在立体几何中仍然成立.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
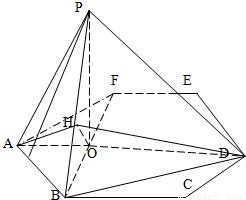
 如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,
如图,P是边长为1的正六边形ABCDEF所在平面外一点,P在平面ABC内的射影为BF的中点O且PO=1,
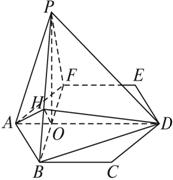
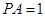 ,P在平面ABC内的射影为BF的中点O。
,P在平面ABC内的射影为BF的中点O。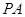 ⊥
⊥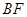 ;
;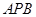 与面
与面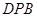 所成二面角的大小。
所成二面角的大小。