题目内容
已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为两切点,则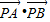 取得最小值时的OP的值为( )
取得最小值时的OP的值为( )A.
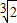
B.
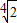
C.
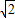
D.
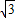
【答案】分析:设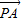 与
与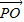 的夹角为α,将
的夹角为α,将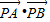 表示成关于tanα的分式函数,令tan2α=x,得
表示成关于tanα的分式函数,令tan2α=x,得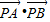 =
=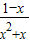 (x>0),利用导数研究它的单调性,可得当x=1+
(x>0),利用导数研究它的单调性,可得当x=1+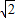 时,即tan2α=1+
时,即tan2α=1+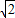 时,
时,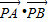 有最小值,由此即可算出|
有最小值,由此即可算出|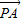 |2=-1+
|2=-1+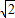 ,由勾股定理可算出此时OP的长,从而得到本题答案.
,由勾股定理可算出此时OP的长,从而得到本题答案.
解答:解:设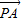 与
与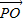 的夹角为α,则|
的夹角为α,则|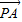 |=|
|=|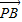 |=
|=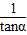
∴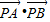 =
=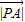 •
•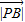 |cos2α|
|cos2α|
=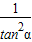 •cos2α=
•cos2α=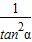 •
•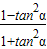 =
=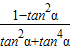
令tan2α=x,得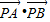 =
=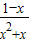 (x>0)
(x>0)
∵f(x)=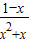 的导数f'(x)=
的导数f'(x)=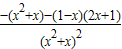 =
=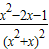
∴0<x<1+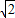 时,f'(x)<0;x>1+
时,f'(x)<0;x>1+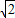 时,f'(x)>0
时,f'(x)>0
可得f(x)在区间(0,1+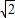 )上是减函数,在区间(1+
)上是减函数,在区间(1+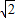 ,+∞)上是增函数
,+∞)上是增函数
∴当x=1+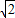 时,即tan2α=1+
时,即tan2α=1+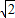 时,
时,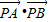 有最小值f(1+
有最小值f(1+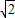 )=-3+2
)=-3+2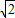
此时,|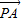 |2=
|2=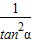 =-1+
=-1+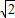 ,可得|OP|=
,可得|OP|=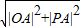 =
=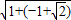 =
=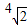
故选:B
点评:本题给出圆外一点P,由P引圆的两条切线,求向量数量积的最小值,着重考查了直线与圆的位置关系、利用导数研究函数的单调性和平面向量数量积的运算等知识,属于中档题.
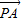 与
与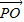 的夹角为α,将
的夹角为α,将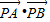 表示成关于tanα的分式函数,令tan2α=x,得
表示成关于tanα的分式函数,令tan2α=x,得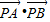 =
=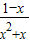 (x>0),利用导数研究它的单调性,可得当x=1+
(x>0),利用导数研究它的单调性,可得当x=1+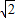 时,即tan2α=1+
时,即tan2α=1+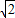 时,
时,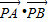 有最小值,由此即可算出|
有最小值,由此即可算出|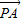 |2=-1+
|2=-1+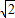 ,由勾股定理可算出此时OP的长,从而得到本题答案.
,由勾股定理可算出此时OP的长,从而得到本题答案.解答:解:设
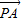 与
与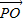 的夹角为α,则|
的夹角为α,则|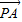 |=|
|=|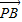 |=
|=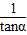
∴
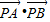 =
=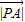 •
•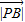 |cos2α|
|cos2α|=
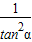 •cos2α=
•cos2α=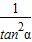 •
•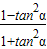 =
=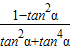
令tan2α=x,得
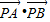 =
=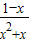 (x>0)
(x>0)∵f(x)=
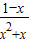 的导数f'(x)=
的导数f'(x)=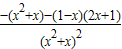 =
=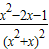
∴0<x<1+
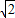 时,f'(x)<0;x>1+
时,f'(x)<0;x>1+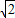 时,f'(x)>0
时,f'(x)>0可得f(x)在区间(0,1+
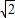 )上是减函数,在区间(1+
)上是减函数,在区间(1+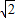 ,+∞)上是增函数
,+∞)上是增函数∴当x=1+
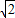 时,即tan2α=1+
时,即tan2α=1+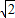 时,
时,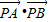 有最小值f(1+
有最小值f(1+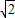 )=-3+2
)=-3+2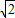
此时,|
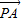 |2=
|2=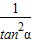 =-1+
=-1+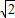 ,可得|OP|=
,可得|OP|=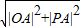 =
=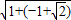 =
=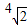
故选:B
点评:本题给出圆外一点P,由P引圆的两条切线,求向量数量积的最小值,着重考查了直线与圆的位置关系、利用导数研究函数的单调性和平面向量数量积的运算等知识,属于中档题.

练习册系列答案
相关题目
已知圆O的半径为1,PA、PB为该圆的两条切线,A、B为两切点,那么
•
的最小值为( )
| PA |
| PB |
A、-4+
| ||
B、-3+
| ||
C、-4+2
| ||
D、-3+2
|