题目内容
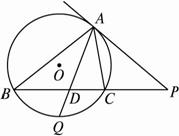
如图2-5，已知△ABC中，∠ABC的平分线交AC于F，交△ABC的外接圆于E，ED切圆于E，交BC的延长线于D.求证：AE2=AF·DE.
图2-5
思路分析:题目中的四条线段不能组成两个相似的三角形，所以利用平行将AE换成EC，根据△AFE∽△ECD，得到比例式，再换回线段即可.
证明:连结EC.∵四边形ABCE内接于⊙O，
∴∠7=∠3＋∠5.
又∵∠5=∠2，∠2=∠1，
∴∠7=∠3＋∠1.
∵∠4=∠3＋∠1，∴∠7=∠4.
∵DE切⊙O于E，EC为弦，
∴∠6=∠5.∴△AFE∽△ECD.
∴
,即AE·EC=DE·AF.
∵∠1=∠2，∴
=
.
∴AE=EC.∴AE2=DE·AF.
练习册系列答案
相关题目
的一个单调递增区间，则b－a的最大值为
,求⊙O的半径.
=
.
=
.?
