题目内容
以点C (t, 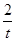 )(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若
)(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若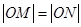 ,则圆C的方程 .
,则圆C的方程 .
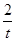 )(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若
)(t∈R , t ≠ 0)为圆心的圆过原点O,直线y = -2x-4与圆C交于点M, N, 若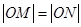 ,则圆C的方程 .
,则圆C的方程 .
试题分析:圆心 C(t,
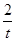 ),半径 r="|OC|="
),半径 r="|OC|="  ,
,因此圆方程为
 ,
,由于
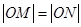 ,|CM|="|CN|" ,所以 OC丄MN ,
,|CM|="|CN|" ,所以 OC丄MN ,则
 ,
,即
 ,解得 t="2" 或 t=" -2" ,
,解得 t="2" 或 t=" -2" ,当 t="2" 时,直线与圆无交点,因此舍去,
所以,圆 C 的方程为
 。
。点评:中档题,利用直线垂直的条件,建立t的方程,注意检验。本题易错,忽视检验。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
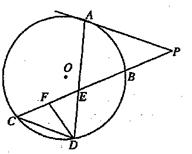
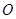 外一点
外一点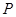 作圆的割线
作圆的割线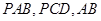 是圆
是圆 ,则
,则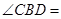 .
.
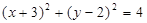 相切的直线方程是___________.
相切的直线方程是___________.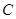 满足以下三个条件:(1)圆心在直线
满足以下三个条件:(1)圆心在直线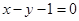 上,(2)与直线
上,(2)与直线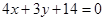 相切,(3)截直线
相切,(3)截直线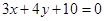 所得弦长为6。求圆
所得弦长为6。求圆 与圆
与圆 相切,则
相切,则 的值为( )
的值为( )


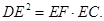
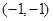 ,B(
,B(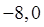 ), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标.
), C(0,6)的圆的方程,并指出这个圆的半径和圆心坐标. 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,
, ,圆
,圆 ,则圆心
,则圆心 的距离为 .
的距离为 .