题目内容
两条平行直线和圆的位置关系定义为:若两条平行直线和圆有四个不同的公共点,则称两条平行线和圆“相交”;若两平行直线和圆没有公共点,则称两条平行线和圆“相离”;若两平行直线和圆有一个、两个或三个不同的公共点,则称两条平行线和圆“相切”.已知直线 ,
, 和圆
和圆 相切,则
相切,则 的取值范围是( )
的取值范围是( )
A.
B. 或
或
C.
D.
【答案】
B
【解析】
试题分析:当两平行直线和圆相交时,有 ,解得
,解得
当两条平行直线和圆相离时 ,解得
,解得 或
或
故当两平行直线和圆相切时,把以上两种情况下求得的 的范围取并集后,再取此并集的补集,即得所求,所求的
的范围取并集后,再取此并集的补集,即得所求,所求的 的最后范围是
的最后范围是 或
或 .
.
考点:1.点到直线的距离公式;2.并集与补集的运算.

练习册系列答案
相关题目
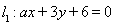
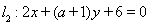
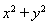
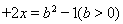
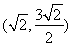
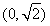

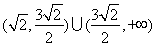
 相切,则a的取值范围是( )
相切,则a的取值范围是( ) B.
B.
 或
或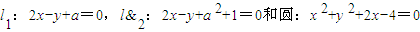 相切,则a的取值范围是( )
相切,则a的取值范围是( )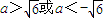
 或
或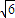 ≤a≤7
≤a≤7