Question

过椭圆的一个焦点且垂直于轴的直线交椭圆于

点.       （Ⅰ）求椭圆C的方程；

（Ⅱ）是否存在过点的直线与椭圆交于两点、，使得（其中为弦的中点）？若存在，求出直线的方程；若不存在，请说明理由

Answer 1

解：（I）依题意，得

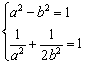．                   …………………3分

解得，．∴椭圆的方程为．………5分

（注：本小题从椭圆定义求解亦可）

（II）设满足条件的直线存在，方程为（必存在），代入椭圆方程，得．  …………………7分

首先，得．             ……………8分

设，，则．… …9分

为的中点，且，

∴．                           ……………………10分

∴

∴

∴

      ∴，满足．   …………12分

∴满足条件的直线存在，方程为．     …………13分

（注：考生对采用其它方法转化，可参照给分