Question

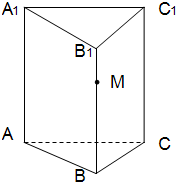如图，已知正三棱柱ABC-A₁B₁C₁的底面边长为1，点M在侧棱BB₁上．
（1）若BM=

2

，求异面直线AM与BC所成的角；
（2）若AB₁⊥BC₁，求棱柱的高BB₁．

Answer 1

分析：（1）利用异面直线的定义，通过做平行线将异面直线所成的角转化为相交直线所成的角问题，通过解三角形求出角的大小．
（2）利用平面垂直的性质得到AF⊥平面BB₁C₁C，利用三垂线定理及逆定理得到CB₁⊥BC₁，得到侧面BB₁C₁C为菱形．

解答：解：（1）过A在平面ABC内作AE∥CB且AE=CB连接EM∠EAM为异面直线AM和BC所成的角或其补角，----（3分）
在△AEM中，AM=EM

12+( 2 )2

=

3

，AE=1，
co∠EAM

3

6

∠EAMaiccos

3

6

--------------（6分）
（2）取BC中点为F，则AF⊥BC，又平面ABC⊥平面BB₁C₁C，
∴AF⊥平面BB₁C₁C，AB₁在平面BB₁C₁C上的射影为B₁F，
∴由已知AB₁⊥BC₁及三垂线定理的逆定理得FB₁⊥BC₁-------------------------（9分）
设BB₁=x
在平面B₁BCC₁中，以B为坐标原点，BC 为x轴建立直角坐标系，则
B（0，0），F（

1

2

，0），B₁（0，x），C₁（1，x）
∵

FB1

⊥BC1
∴(1，x)•(

1

2

，-x)=0
∴x=

2

2

∴BB1=

2

2

-------------------------（12分）

点评：解决异面直线所成的角，常通过作平行线转化为相交直线所成的角；有时也常利用向量来解决．注意异面线所成角的范围．