Question

已知抛物线y²=6x,过点P(4,1)引一弦,使它恰被点P平分,求这条弦所在的直线方程.

Answer 1

解法一:设直线上任意一点坐标为(x,y),弦的两个端点为P₁(x₁,y₁)、P₂(x₂,y₂).

∵P₁、P₂在抛物线上,

∴y₁²=6x₁,y₂²=6x₂.

两式相减,得(y₁+y₂)(y₁-y₂)=6(x₁-x₂),                                ①

∵y₁+y₂=2,代入①,得

∴直线的方程为y-1=3(x-4),即3x-y-11=0.

解法二:设所求方程为y-1=k(x-4).

由方程组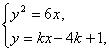得ky²-6y-24k+6=0.

设弦的两端点P₁、P₂的坐标分别是(x₁,y₁)、(x₂,y₂),则y₁+y₂=.

∵P₁P₂的中点为(4,1),∴=2.∴k=3.

∴所求直线方程为y-1=3(x-4),即3x-y-11=0.