题目内容
7.已知F1,F2分别是双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,A是曲线在第一象限内的点,若|AF2|=2,且∠F1AF2=45°,延长AF2交双曲线右支于点B,则|BF2|=2$\sqrt{2}$-2.分析 画出草图,结合双曲线的定义可知AF1=4,设BF2=x,则BF1=x+2,在△ABF1中利用余弦定理可解出x
解答  解:
解:
∵AF1-AF2=2,BF1-BF2=2,
∴AF1=AF2+2=4,设BF2=x,则BF1=x+2,
在△ABF1中,由余弦定理得:
(x+2)2=16+(x+2)2-8(x+2)cos45°
解得x=2$\sqrt{2}$-2.
故答案为2$\sqrt{2}$-2.
点评 本题考查了双曲线的定义,是基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.不等式$\frac{3-4x}{1-2x}$≤1的解集为( )
| A. | [1,+∞) | B. | ($\frac{1}{2}$,1) | C. | [$\frac{1}{2}$,1] | D. | ($\frac{1}{2}$,1] |
15.函数y=cos(x+$\frac{π}{6}$),x∈[0,$\frac{π}{2}$].的值域是( )
| A. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$] | C. | [$\frac{\sqrt{3}}{2}$,1] | D. | [$\frac{1}{2}$,1] |
2.下面几个空间图形中,虚线、实线使用不正确的有( )
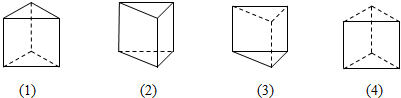

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |
16.设i是虚数单位,则复数z=$\frac{5}{i(i+2)}$的虚部为( )
| A. | -2 | B. | 2 | C. | -1 | D. | -2i |
 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为F,过点F的直线交椭圆于A,B两点,|AF|的最大值为M,|BF|的最小值为m,满足$M•m=\frac{3}{4}{a^2}$.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左焦点为F,过点F的直线交椭圆于A,B两点,|AF|的最大值为M,|BF|的最小值为m,满足$M•m=\frac{3}{4}{a^2}$.