题目内容
关于函数f(x)=4sin(2x+
)(x∈R),有下列命题:
①y=f(x)的表达式可改写为y=4cos(2x-
);
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点(-
,0)对称;
④y=f(x)的图象关于直线x=-
对称.
其中正确的命题的序号是______.
| π |
| 3 |
①y=f(x)的表达式可改写为y=4cos(2x-
| π |
| 6 |
②y=f(x)是以2π为最小正周期的周期函数;
③y=f(x)的图象关于点(-
| π |
| 6 |
④y=f(x)的图象关于直线x=-
| π |
| 6 |
其中正确的命题的序号是______.
∵f (x)=4sin(2x+
)=4cos(
-2x-
)=4cos(-2x+
)=4cos(2x-
),故①正确;
∵T=
=π,故②不正确;
令x=-
代入f (x)=4sin(2x+
)得到f(-
)=4sin(-
-
)=0,故y=f (x)的图象关于点(-
, 0)对称,③正确④不正确;
故答案为:①③.
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
∵T=
| 2π |
| 2 |
令x=-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
故答案为:①③.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 )(
)( ),有下列命题:
),有下列命题: 可得
可得 必是
必是 的整数倍;
的整数倍;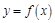 的表达式可改写为
的表达式可改写为 ;
; 对称;
对称; 对称.
对称.