Question

(本题满分12分)

已知直线l：mx–2y+2m=0(mR)和椭圆C：(a>b>0), 椭圆C的离心率为，连接椭圆的四个顶点形成四边形的面积为2.

（I）求椭圆C的方程；

（II）设直线l经过的定点为Q，过点Q作斜率为k的直线l^/与椭圆C有两个不同的交点，求实数k的取值范围；

(Ⅲ)设直线l与y轴的交点为P，M为椭圆C上的动点，线段PM长度的最大值为f(m)，求f(m)的表达式.

Answer 1

(本题满分12分)

（I）由离心率，得

又因为，所以，

即椭圆标准方程为.                          4分

（II）由l：mx–2y+2m=0经过定点Q(–2, 0),  则直线l^/：y=k(x+2)， 

  由 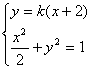  有．

    所以，  可化为

    解得．                                  8分

(Ⅲ) 由l：mx–2y+2m=0，设x=0, 则y=m, 所以P(0, m).

设M(x, y)满足,

则|PM|² =x² +(y –m)² =2–2y² +(y – m )² = –y² –2my +m²+2

      = –(y +m)² +2m² +2， 因为 –1y1,  所以

 当|m|>1时，|MP|的最大值f(m)=1+|m|；

 当|m|1时，|MP|的最大值f(m)=；

所以f(m)=.                         12分