题目内容
 如图,椭圆
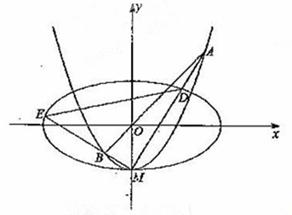
如图,椭圆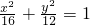 的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点,则此二面角的大小为________.
的长轴为A1A2,短轴为B1B2,将坐标平面沿y轴折成一个二面角,使点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点,则此二面角的大小为________.

分析:确定椭圆中的几何量,确定二面角的平面角,利用点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点,可求得cos∠A2OF1=
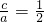 ,即可求得结论.
,即可求得结论.解答:由题意,椭圆
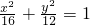 中a=4,c=
中a=4,c= ,∠A2OF1为二面角的平面角
,∠A2OF1为二面角的平面角∵点A2在平面B1A1B2上的射影恰好是该椭圆的左焦点
∴在直角△A2OF1中,cos∠A2OF1=
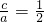
∴∠A2OF1=

即二面角的大小为

故答案为:

点评:本题考查椭圆与立体几何的综合,考查面面角,解题的关键是确定二面角的平面角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
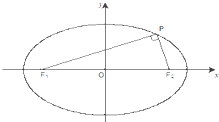 如图,椭圆的标准方程为
如图,椭圆的标准方程为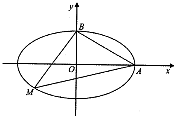 (2012•厦门模拟)某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米.现以椭圆长轴所在直线为x轴,短轴所在直线为y轴,建立平面直角坐标系,如图所示.
(2012•厦门模拟)某公园内有一椭圆形景观水池,经测量知,椭圆长轴长为20米,短轴长为16米.现以椭圆长轴所在直线为x轴,短轴所在直线为y轴,建立平面直角坐标系,如图所示. 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=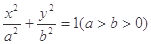 的长轴为AB,过点B的直线
的长轴为AB,过点B的直线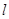 与
与
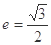 ,F为椭圆的左焦点,且
,F为椭圆的左焦点,且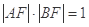
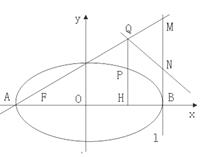
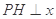 轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线
轴,H为垂足,延长HP到点Q,使得HP=PQ,连接AQ并延长交直线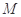 ,
,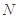 为
为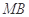 的中点,判定直线
的中点,判定直线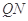 与以
与以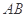 为直径的圆O位置关系。
为直径的圆O位置关系。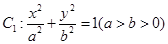 的离心率为
的离心率为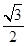 ,
,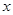 轴被曲线
轴被曲线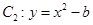 截得的线段长等于
截得的线段长等于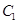 的长半轴长.
的长半轴长.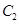 的方程;
的方程;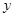 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线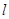 与
与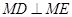 ;
;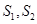 .问:是否存在直线
.问:是否存在直线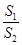 =
= ?请说明理由.
?请说明理由.