题目内容
已知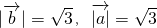 ,
,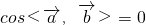 ,若向量
,若向量 满足
满足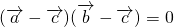 ,则
,则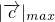 =
=
- A.

- B.2
- C.

- D.

C
分析:由题意可得 =0,再由
=0,再由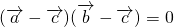 ,求得
,求得 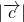 =|
=|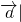 cosα+|
cosα+| |cosβ=
|cosβ= cosα+
cosα+ cosβ,由于α+β=
cosβ,由于α+β= 或α+β=
或α+β= ,故有cosβ=sinα 或cosβ=-sinα,从而得到
,故有cosβ=sinα 或cosβ=-sinα,从而得到 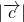 =
=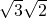 sin(α±
sin(α± )≤
)≤ ,由此得到答案.
,由此得到答案.
解答:∵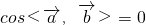 ,∴
,∴ ,∴
,∴ =0.
=0.
∵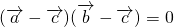 ,∴
,∴ -
- -
-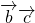 +
+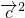 =0-
=0-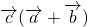 +
+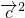 =0.
=0.
∴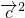 =
= +
+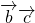 =|
=|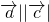 cosα+
cosα+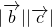 cosβ,其中α、β分别是
cosβ,其中α、β分别是 与
与 ,
, 与
与 的夹角,
的夹角,
故有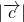 =|
=|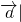 cosα+|
cosα+| |cosβ=
|cosβ= cosα+
cosα+ cosβ.
cosβ.
由题意可得 α+β= 或α+β=
或α+β= .
.
当 α+β= 时,cosβ=sinα,∴
时,cosβ=sinα,∴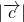 =
= (cosα+cosβ )=
(cosα+cosβ )= (cosα+sinα )=
(cosα+sinα )=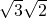 sin(α+
sin(α+ )≤
)≤ .
.
当α+β= 时,cosβ=-sinα,∴
时,cosβ=-sinα,∴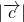 =
= (cosα+cosβ )=
(cosα+cosβ )= (cosα-sinα )=
(cosα-sinα )=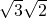 sin(α-
sin(α- )≤
)≤ .
.
故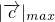 =
= ,
,
故选C
点评:本题主要考查两个向量的数量积的定义,辅助角公式,两个向量垂直的性质,属于中档题.
分析:由题意可得
 =0,再由
=0,再由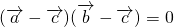 ,求得
,求得 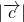 =|
=|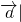 cosα+|
cosα+| |cosβ=
|cosβ= cosα+
cosα+ cosβ,由于α+β=
cosβ,由于α+β= 或α+β=
或α+β= ,故有cosβ=sinα 或cosβ=-sinα,从而得到
,故有cosβ=sinα 或cosβ=-sinα,从而得到 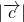 =
=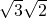 sin(α±
sin(α± )≤
)≤ ,由此得到答案.
,由此得到答案.解答:∵
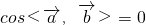 ,∴
,∴ ,∴
,∴ =0.
=0.∵
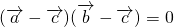 ,∴
,∴ -
- -
-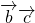 +
+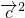 =0-
=0-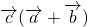 +
+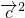 =0.
=0.∴
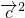 =
= +
+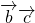 =|
=|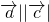 cosα+
cosα+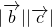 cosβ,其中α、β分别是
cosβ,其中α、β分别是 与
与 ,
, 与
与 的夹角,
的夹角,故有
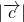 =|
=|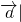 cosα+|
cosα+| |cosβ=
|cosβ= cosα+
cosα+ cosβ.
cosβ.由题意可得 α+β=
 或α+β=
或α+β= .
.当 α+β=
 时,cosβ=sinα,∴
时,cosβ=sinα,∴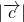 =
= (cosα+cosβ )=
(cosα+cosβ )= (cosα+sinα )=
(cosα+sinα )=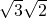 sin(α+
sin(α+ )≤
)≤ .
.当α+β=
 时,cosβ=-sinα,∴
时,cosβ=-sinα,∴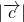 =
= (cosα+cosβ )=
(cosα+cosβ )= (cosα-sinα )=
(cosα-sinα )=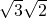 sin(α-
sin(α- )≤
)≤ .
.故
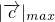 =
= ,
,故选C
点评:本题主要考查两个向量的数量积的定义,辅助角公式,两个向量垂直的性质,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目