题目内容
设函数![]() ,
,![]() ,已知
,已知![]() 与
与![]() 有且仅有一个公共点.
有且仅有一个公共点.
(1)求m的值;
(2)对于函数![]() ,若存在a,b,使得关于
,若存在a,b,使得关于![]() 的不等式
的不等式![]() 对于
对于![]() 定义域上的任意实数
定义域上的任意实数![]() 恒成立,求a的最小值以及对应的
恒成立,求a的最小值以及对应的![]() 的解析式.
的解析式.
(1)令![]() ,即
,即![]() ,
,
可得![]() ,设
,设![]() ,
,
则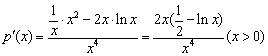 ,
,
令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 递增;当
递增;当![]() 时,
时,![]() ,
,![]() 递减.
递减.
考虑到![]() 时,,
时,,
![]() 时,
时,![]() ;
;
![]() 时,
时,![]() .
.
考虑到![]() ,故
,故![]() ,因此
,因此![]() .………………………………4分
.………………………………4分
(2)由(1)知,![]() .
.
![]() ,可知
,可知![]() . ………………………………6分
. ………………………………6分
(ⅰ)由![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
所以![]() ,解得
,解得![]() ①.……………………8分
①.……………………8分
(ⅱ)由![]() 对
对![]() 恒成立,
恒成立,
即![]() 对
对![]() 恒成立,
恒成立,
设![]() ,
,![]() ,
,
则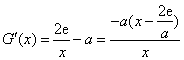 ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,
,![]() 递增;当
递增;当![]() 时,
时,![]() ,
,![]() 递减.
递减.
故![]() ,
,
则须![]() ,即得
,即得![]() ②.
②.
由①②得![]() ③. ……………………10分
③. ……………………10分
存在a,b,使得③成立的充要条件是:不等式![]() ④有解.
④有解.
……………………12分
不等式④可化为![]() ,即
,即![]() ,
,
令![]() ,则有
,则有![]() ,设
,设![]() ,
,
则![]() ,
,
可知![]() 在
在![]() 上递增,
上递增,![]() 上递减.
上递减.
又![]() ,
,![]() ,
,![]() ,
,
所以![]() 在区间
在区间![]() 内存在一个零点
内存在一个零点![]() ,
,
故不等式![]() 的解为
的解为![]() ,即
,即![]() ,得
,得![]() .
.
因此a的最小值为2,代入③得![]() ,故
,故![]() ,
,
对应的![]() 的解析式为
的解析式为![]() . ………………………………16分
. ………………………………16分

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
 函数
函数 在
在 上单调递减;命题
上单调递减;命题 关于x的不等式
关于x的不等式 的解集为R。若命题
的解集为R。若命题 与
与 有且仅有一个正确,求
有且仅有一个正确,求 的取值范围。
的取值范围。 函数
函数 在
在 上单调递减;命题
上单调递减;命题 关于x的不等式
关于x的不等式 的解集为R。若命题
的解集为R。若命题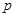 与
与 有且仅有一个正确,求
有且仅有一个正确,求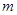 的取值范围。
的取值范围。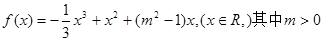 .
.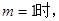 曲线
曲线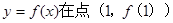 处的切线斜率;
处的切线斜率;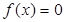 有三个互不相同的实根0,
有三个互不相同的实根0,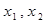 ,且
,且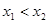 .若对任意的
.若对任意的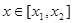 ,
,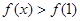 恒成立,求m的取值范围
恒成立,求m的取值范围