题目内容
已知函数f（x）=
有极值，且在x=-1处的切线与直线x-y+1=0 平行。
（Ⅰ）求实数a的取值范围；
（Ⅱ）是否存在实数a，使得f’（x）= x的两个根
满足
，若存在，求实数a的取值范围；若不存在，请说明理由。
解：（Ⅰ）
.
由题意，
，
令
，即x2+ax+a=0，
（1）当△=a2-4a≤0时，
恒成立，y=f(x)没有极值.
（2）当△=a2-4a>0，即a<0,或a>4时，有两个不相等的实数根，
y=f(x)有极值.
综上，a的取值范围是
.
（Ⅱ）假设存在实数a，使
的两根满足0<x1<x2<1，
即x2+(a-1)x+a=0的两根满足. 0<x1<x2<1
令g(x)=x2+(a-1)x+a，
则
解得
.
与（Ⅰ）中a<0,或a>4矛盾.
因此，符合条件的实数a不存在.
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
已知函数f（x）=loga（2+x）-loga（2-x）（a＞0，a≠1），设f（x）的反函数为f-1（x）．若关于x的不等式f-1（x）＜m（m∈R）有解，则m的取值范围是（ ）
| A、m＞-2 | B、m＞2 | C、-2＜m＜2 | D、随a的变化而变化 |
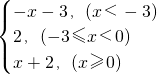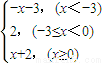，有下面四个结论：
，有下面四个结论：
，有下面四个结论：