题目内容
已知f（x）是偶函数，它在[0，+∞）上是增函数，若f（lgx）＜f（1），则x的取值范围是 ．
【答案】分析：根据偶函数的性质及单调性，f（lgx）＜f（1）等价于|lgx|＜1，由此可求x的取值范围．
解答：解：∵f（x）是偶函数，它在[0，+∞）上是增函数，
∴f（lgx）＜f（1）等价于|lgx|＜1，
∴-1＜lgx＜1
∴
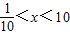
∴x的取值范围是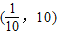
故答案为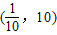
点评：本题考查函数单调性与奇偶性的结合，考查学生转化问题的能力，属于中档题．
解答：解：∵f（x）是偶函数，它在[0，+∞）上是增函数，
∴f（lgx）＜f（1）等价于|lgx|＜1，
∴-1＜lgx＜1
∴
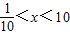
∴x的取值范围是
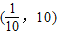
故答案为
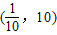
点评：本题考查函数单调性与奇偶性的结合，考查学生转化问题的能力，属于中档题．
练习册系列答案
中考利剑中考试卷汇编系列答案
相关题目
已知f（x）是偶函数，且f（x）在[0，+∞）上是增函数，如果f（ax+1）≤f（x-2）在x∈[
，1]上恒成立，则实数a的取值范围是（ ）
| 1 |
| 2 |
| A、[-2，1] |
| B、[-5，0] |
| C、[-5，1] |
| D、[-2，0] |