Question

如图，在三棱锥O-ABC中，三条棱OA，OB，OC两两垂直，且OA＞OB＞OC，分别经过三条棱OA，OB，OC作一个截面平分三棱锥的体积，截面面积依次为S₁，S₂，S₃，则S₁，S₂，S₃的大小关系为

 

．

Answer 1

分析：设OA=a、OB=b、OC=c，取BC的中点D并连结OD、AD，由三角形中线的性质与锥体体积公式，可得截面OAD就是将三棱锥O-ABC的体积分成两等分的截面三角形，结合题意得S_△OAD=S₁．根据OA、OB、OC两两垂直，在Rt△OBC中算出中线OD=

1

2

b2+c2

，从而算出Rt△AOD的面积S₁=

1

4

a2b2+a2c2

．同理求出S₂=

1

4

a2b2+b2c2

，S₃=

1

4

b2c2+a2c2

．最后根据a＞b＞c＞0比较三个表达式的大小，即可得到S₁＞S₂＞S₃．

解答：解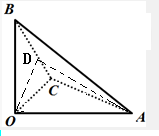：设OA=a，OB=b，OC=c，则a＞b＞c＞0．取BC的中点D，连结OD、AD，
∵OD是△BCD的BC边上的中线，
∴S_△OBD=S_△OCD=

1

2

S_△OBC，因此V_A-OBD=V_A-OCD=

1

2

V_A-OBC，
即截面OAD将三棱锥O-ABC的体积分成两等分，可得S_△OAD=S₁，
∵OA、OB、OC两两垂直，∴OA⊥OB，OB⊥OC且OA⊥OC，
∵OB、OC是平面OBC内的相交直线，
∴OA⊥平面OBC，结合OD?平面OBC，得OA⊥OD．
∵Rt△OBC中，OB=b且OC=c，∴斜边BC=

b2+c2

，得OD=

1

2

BC=

1

2

b2+c2

．
因此S_△OAD=

1

2

OA•OD=

1

4

a2b2+a2c2

，即S₁=

1

4

a2b2+a2c2

．
同理可得S₂=

1

4

a2b2+b2c2

，S₃=

1

4

b2c2+a2c2

．
∵a＞b＞c＞0，
∴a²b²+a²c²＞a²b²+b²c²＞b²c²+a²c²，
可得

1

4

a2b2+a2c2

＞

1

4

a2b2+b2c2

＞

1

4

b2c2+a2c2

，即S₁＞S₂＞S₃．
故答案为：S₁＞S₂＞S₃

点评：本题给出过同一个顶点三条棱两两垂直的三棱锥，经过这三条棱分别作将三棱锥分成两等分的截面，比较三个截面的大小．着重考查了线面垂直的判定与性质、锥体的体积公式、勾股定理与解直角三角形和不等式的性质等知识，属于中档题．