题目内容
10.已知$\frac{4}{x}+\frac{9}{y}$=1,且x>0,y>0,则x+y的最小值是25.分析 由题意可得x+y=($\frac{4}{x}+\frac{9}{y}$)(x+y)=13+$\frac{4y}{x}$+$\frac{9x}{y}$,由基本不等式可得.
解答 解:∵$\frac{4}{x}+\frac{9}{y}$=1,且x>0,y>0,
∴x+y=($\frac{4}{x}+\frac{9}{y}$)(x+y)
=13+$\frac{4y}{x}$+$\frac{9x}{y}$≥13+2$\sqrt{\frac{4y}{x}•\frac{9x}{y}}$=25
当且仅当$\frac{4y}{x}$=$\frac{9x}{y}$即x=10且y=15时取等号.
故选答案为:25.
点评 本题考查基本不等式求最值,“1”的整体代换是解决问题的关键,属基础题.

练习册系列答案
相关题目
1.“a>b”是“2a>2b”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.已知双曲线x${\;}^{2}-\frac{{y}^{2}}{{b}^{2}}=1$(b>0),若右焦点F(c,0)到一条渐近线的距离为2,则双曲线的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\sqrt{5}$ |
19.下列函数中最小正周期为π,且为偶函数的是( )
| A. | y=$\frac{1}{2}$|sinx| | B. | $y=\frac{1}{2}cos(2x+\frac{π}{2})$ | C. | y=tanx | D. | y=cos$\frac{1}{3}$x |
20.若幂函数f(x)的图象过点(2,8),则f(3)的值为( )
| A. | 6 | B. | 9 | C. | 16 | D. | 27 |
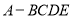 中, 底面
中, 底面 为菱形,侧面
为菱形,侧面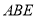 为等边三角形,且侧面
为等边三角形,且侧面 底面
底面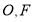 分别为
分别为 的中点.
的中点.
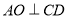 ;
;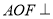 平面
平面 ;
; 上是否存在点
上是否存在点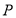 ,使得
,使得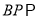 平面
平面 ?若存在,求出
?若存在,求出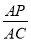 的值; 若不存在,请说明理由.
的值; 若不存在,请说明理由.