题目内容
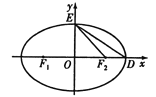
【题目】如图![]() 为椭圆C:
为椭圆C:![]()
![]() 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率![]() ,
,![]() 的面积为
的面积为![]() .若点
.若点![]() 在椭圆C上,则点
在椭圆C上,则点![]() 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线![]() 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
(1)求椭圆C的标准方程;
(2)问是否存在过左焦点![]() 的直线
的直线![]() ,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
,使得以PQ为直径的圆经过坐标原点?若存在,求出该直线的方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)直线方程为
;(2)直线方程为![]() 或
或![]() .
.
【解析】
试题分析:本题主要考查椭圆的标准方程、直线的标准方程、圆的标准方程、韦达定理、向量垂直的充要条件等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用椭圆的离心率和三角形面积公式列出表达式,解方程组,得到基本量a和b的值,从而得到椭圆的方程;第二问,直线l过左焦点,所以讨论直线的斜率是否存在,当斜率不存在时,可以直接写出直线方程,令直线与椭圆联立,得到交点坐标,验证以PQ为直径的圆不过坐标原点,当斜率存在时,直线与椭圆联立,消参,利用韦达定理,证明![]() ,解出k的值.
,解出k的值.
(1)由题意,![]() ,即
,即![]() ,
,![]() ,即
,即![]() 2分
2分
又![]() 得:
得: ![]()
∴椭圆![]() 的标准方程:
的标准方程:![]() . 5分
. 5分
(2)①当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]()
联立 ,解得
,解得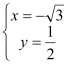 或
或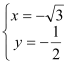 ,
,
不妨令![]() ,
,![]() ,所以对应的“椭点”坐标
,所以对应的“椭点”坐标![]() ,
,![]() .
.
而![]()
所以此时以![]() 为直径的圆不过坐标原点. 7分
为直径的圆不过坐标原点. 7分
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]()
 消去
消去![]() 得,
得,![]()
设![]() ,则这两点的“椭点”坐标分别为
,则这两点的“椭点”坐标分别为![]()
由根与系数关系得:![]() 9分
9分
若使得以![]() 为直径的圆过坐标原点,则
为直径的圆过坐标原点,则![]()
而![]() ,∴
,∴![]()
即![]() ,即
,即![]()
代入![]() ,解得:
,解得:![]()
所以直线方程为![]() 或
或![]() . 12分
. 12分

练习册系列答案
相关题目