题目内容
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.直线
上.直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(Ⅱ)点![]() 为坐标原点,延长线段
为坐标原点,延长线段![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求出此时直线
能否为平行四边形?若能,求出此时直线![]() 的方程,若不能,说明理由.
的方程,若不能,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】
(I)根据已知得到a,b,c的方程组,解方程组即得椭圆的标准方程;(Ⅱ)先讨论当直线![]() 与
与![]() 轴垂直时,直线
轴垂直时,直线![]() 的方程为
的方程为![]() 满足题意.再讨论直线
满足题意.再讨论直线![]() 与
与![]() 轴不垂直,设直线
轴不垂直,设直线![]() ,先计算出
,先计算出![]() ,
,![]() ,再根据
,再根据![]() 求出此时直线
求出此时直线![]() 的方程.
的方程.
解:(I)由题意得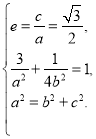 ,解得
,解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]()
(Ⅱ)四边形![]() 能为平行四边形.
能为平行四边形.
(1)当直线![]() 与
与![]() 轴垂直时,直线
轴垂直时,直线![]() 的方程为
的方程为![]() 满足题意
满足题意
(2)当直线![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() ,显然
,显然![]() .
.
设![]() ,
,![]() ,
,![]() .
.
将![]() 代入
代入![]() 得
得![]() ,
,
![]() 故
故![]() ,
,
![]() .于是直线
.于是直线![]() 的斜率
的斜率![]() ,即
,即![]() .
.
由直线![]()
![]() ,过点
,过点![]() ,得
,得![]() ,因此
,因此![]() .
.
![]() 的方程为
的方程为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() .
.
由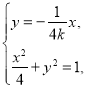 得
得![]() ,即
,即![]() .
.
四边形![]() 为平行四边形当且仅当线段
为平行四边形当且仅当线段![]() 与线段
与线段![]() 互相平分,即
互相平分,即![]() .
.
于是![]()
![]() .由
.由![]() ,得
,得![]() 满足
满足![]()
所以直线![]() 的方程为
的方程为![]() 时,四边形
时,四边形![]() 为平行四边形.
为平行四边形.
综上所述:直线![]() 的方程为
的方程为![]() 或
或![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目